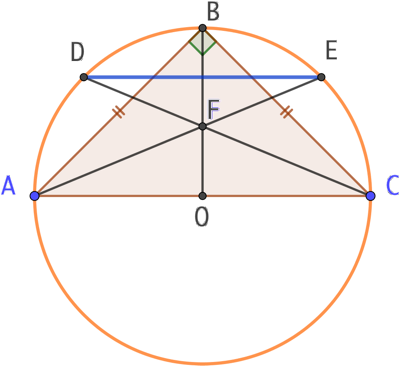
 Soit un triangle ABC isocèle et rectangle en B. On trace ses trois bissectrices qui se coupent au point F. alors les droites (AC) et (DE) sont parallèles.
Soit un triangle ABC isocèle et rectangle en B. On trace ses trois bissectrices qui se coupent au point F. alors les droites (AC) et (DE) sont parallèles.
Explications :
Il suffit de vérifier que les angles alternes-externes ![]() et
et ![]() sont de même mesure.
sont de même mesure.
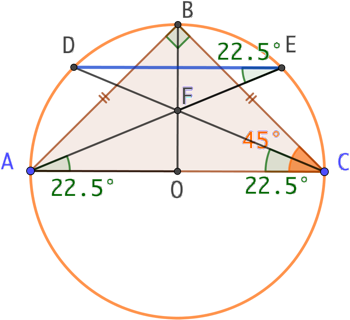
![]() et
et ![]() interceptent le même arc AD et sont donc de même mesure.
interceptent le même arc AD et sont donc de même mesure.
ABC étant un triangle isocèle rectangle, ![]() . (DC) étant une bissectrice de
. (DC) étant une bissectrice de ![]() , il vient que l’angle
, il vient que l’angle ![]() = 22,5°. Il en va donc de même pour l’angle
= 22,5°. Il en va donc de même pour l’angle ![]() .
.
(AE) étant a bissectrice de ![]() , il vient que
, il vient que ![]() . Donc
. Donc ![]() . On en conclut que les droites (AC) et (DE) sont parallèles.
. On en conclut que les droites (AC) et (DE) sont parallèles.
