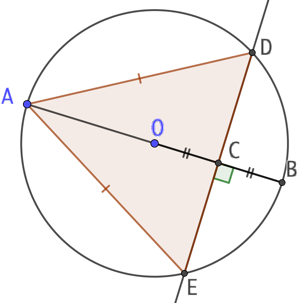
 Étant donné un cercle de centre O, on construit un triangle équilatéral ainsi :
Étant donné un cercle de centre O, on construit un triangle équilatéral ainsi :
- On choisit un point quelconque A sur le cercle.
- À partir de A, on trace un diamètre du cercle qui coupe le cercle au point B.
- On place C, milieu du segment [OB].
- On trace la perpendiculaire à (OB) qui passe par C. Celle-ci coupe le cercle aux points D et E. ADE est un triangle équilatéral.
Explications :
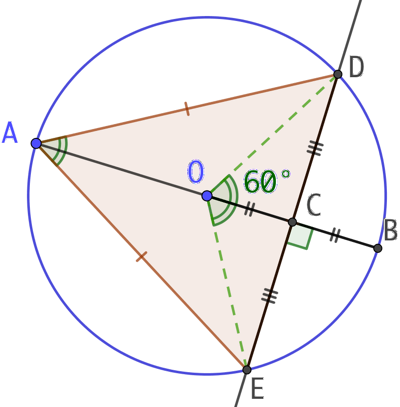
![]() car C est le milieu de [OB] donc
car C est le milieu de [OB] donc ![]() .
.
Comme ![]() est un angle aigus, on peut affirmer que
est un angle aigus, on peut affirmer que ![]() mesure 60°.
mesure 60°.
On démontre à l’identique que l’angle ![]() mesure également 60°. Cela implique que :
mesure également 60°. Cela implique que :
- l’angle
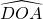 mesure 180 – 60 = 120° ;
mesure 180 – 60 = 120° ; - l’angle
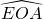 mesure 180 – 60 = 120°.
mesure 180 – 60 = 120°.
En résumé, les trois triangles ODA, OAE et OED ont un angle au sommet de même mesure (120°) et des côtés adjacents aux angles au sommet de même longueur (le rayon du cercle). Ces trois triangles sont donc isométriques et leur troisième côté, AD, AE et ED, sont de même longueur. On peut alors affirmer que ADE est un triangle équilatéral.
