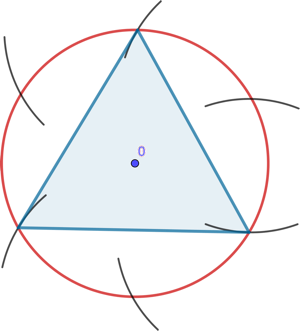
Étant donné un cercle de centre O, on construit un triangle équilatéral à l’aide du seul compas comme outil ainsi :
- On trace le cercle de centre O et on maintient l’écartement du compas à l’identique.
- On choisit un point quelconque sur le cercle. on trace un arc de cercle à partir de ce point qui rencontre le cercle.
- On reproduit cette opération à partir du nouveau point obtenu sur le cercle.
- Quand on a obtenu six points sur le cercle, on en choisit un sur deux pour tracer trois cordes qui forme un triangle équilatéral.
Explications :
On complète la figure en traçant les six segments reliant les six points déterminés au compas. On notre au passage qu’on vient ainsi de tracer un hexagone régulier.
Les trois quadrilatères OAFE, OEDC et OCBA sont des losanges isométriques puisque tous leurs côtés sont, soit des rayons du cercle, soit des segments de longueur égale au rayon du cercle.
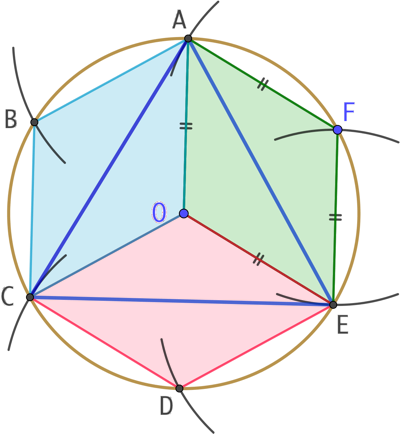Les trois côtés du triangle ACE sont les grandes diagonales des trois losanges. Elles sont de même longueur puisque les trois losanges sont isométriques. ACE est donc un triangle équilatéral.
