 Etant donné un carré ABCD, on construit un rectangle dont la longueur BE est donnée et dont l’aire est égale à celle du carré :
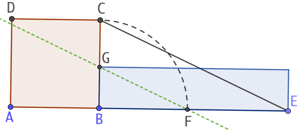
Etant donné un carré ABCD, on construit un rectangle dont la longueur BE est donnée et dont l’aire est égale à celle du carré :
- On trace le segment [CE].
- On trace un arc de cercle de centre B et de rayon la longueur du côté du carré afin de placer le point F sur la droite (AB).
- On trace la droite passant par F et parallèle à (CE). Elle rencontre le segment [BC] au point G. La distance BG est la longueur de la largeur du rectangle cherché.
- Pour terminer la construction du rectangle, il suffit ensuite de mener la droite parallèle à (BE) passant par G et la droite parallèle (BC) passant par E.
 Explications :
Explications :
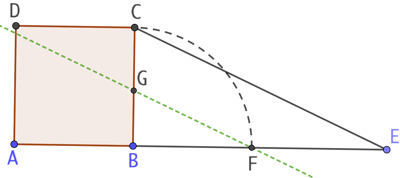
Par construction les droites (CE) et (GF) sont parallèles. On utilise le théorème de Thales dans le triangle BEC. On a l’égalité de rapports : BG / BC = BF / BE soit BG = BC2 / BE puisque BF = BC par construction. BC2 représente l’aire du carré, donc celle du rectangle. On retrouve le résultat attendu à savoir que la largeur du rectangle est égale au quotient de son aire par sa longueur.
