Dans un triangle quelconque, la sommes des distances du centre du cercle circonscrit aux côtés du triangle est égale à la somme des rayons du cercle circonscrit et du cercle inscrit.
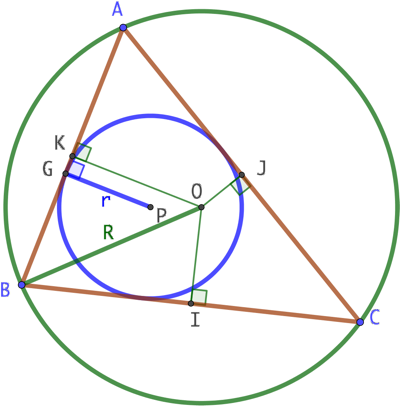
Construction :
- ABC un triangle quelconque.
- Le cercle inscrit dans ABC de centre P et de rayon r.
- Le cercle circonscrit de centre O dont le rayon est R = OB.
- I, J et K, projections orthogonales de O sur les trois côtés de ABC.
L’égalité du théorème japonais de Carnot : 
.
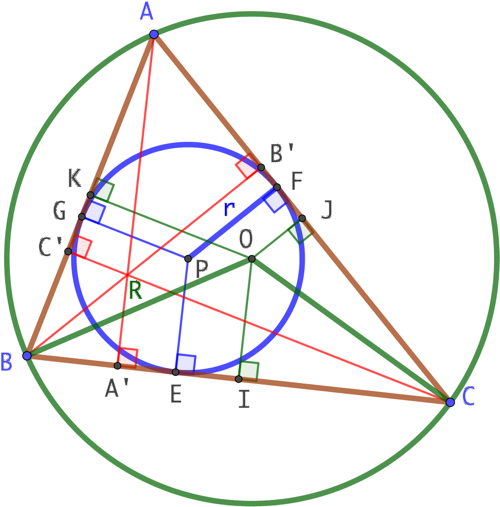
Construction complémentaire pour les explications :
- E, F et G, projections orthogonales de P sur les trois côtés de ABC.
- I, J et K, projections orthogonales de O sur les trois côtés de ABC.
- A’, B’ et C’, pieds des hauteurs issues de A, B et C.
Explications :
Puisque P est le centre du cercle inscrit dans ABC :
- l’aire de PBC est
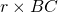
- l’aire de PCA est
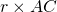
- l’aire de PAB est
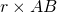
Donc l’aire de ABC est 
si on pose 
.
Puisque O est le centre du cercle circonscrit de ABC :
- l’aire de OBC est
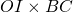
- l’aire de OCA est
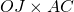
- l’aire de OAB est
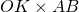
Donc l’aire de ABC est 
.
En rapprochant les deux expressions de l’aire de ABC on obtient :
(1) 
Les triangles rectangles ABB’ et ACC’ sont semblables puisqu’ils ont un angle commun : 
. Donc 
soit = 
.
Par ailleurs l’angle inscrit 
et l’angle au centre 
interceptent le même arc de cercle BC. Donc 
.
Or BOC est un triangle isocèle en O donc 
. D’où l’égalité : 
.
Comme 
, il vient que 
, soit 
.
On démontrerait de la même façons que :
En additionnant ces trois égalités on obtient après simplification :
(2) 
.
En additionnant membre à membre les égalités (1) et (2), on trouve après mise en facteur de 
et simplification : 
