Premier résultat
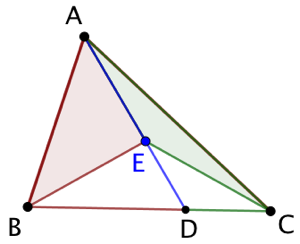
Soient un point E à l’intérieur d’un triangle ABC et D le point d’intersection de (AE) et (BC). Le rapport des aires des triangles ABE et AEC est égal à celui de BD et DC.
Explications :
En considérant le triangle ABC : 
.
Et en considérant le triangle EBC : 
.
Par conséquent : 
Rappel d’une propriété : 
Conclusion : 
.
Second résultat
Le rapport des aires des triangles BEC et BAC est égal à celui de DE et DA.
Explications :
En considérant le triangle ABD : 
.
Et en considérant le triangle ADC : 
.
Par conséquent : 
Rappel d’une propriété : 
Conclusion : 
.
