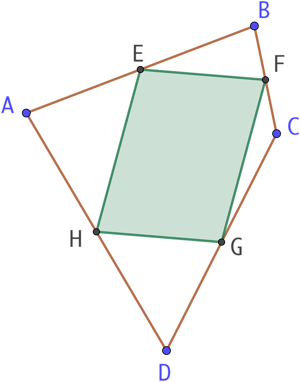
Étant donné un quadrilatère quelconque ABCD et les milieux E, F, G et H de ses quatre côtés, on démontre que le quadrilatère EFGH est un parallélogramme.
Explications :
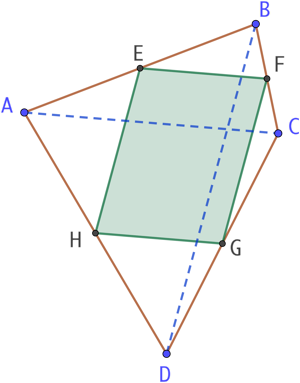
On complète la figure en traçant les diagonales [AC] et [BD] de ABCD. On applique ensuite le théorème des milieux.
Dans le triangle ABC, E et F étant les milieux respectifs de [BA] et [BC], nous pouvons, grâce au théorème des milieux, affirmer que :
- les droites (EF) et (AC) sont parallèles ;
- AC = 2 x EF.
Dans le triangle ADC, H et G étant les milieux respectifs de [DA] et [DC], Par conséquent :
- les droites (HG) et (AC) sont parallèles ;
- AC = 2 x HG.
De ce qui précède, il vient que :
- les droites (EF) et (HG) sont parallèles ;
- EF = HG.
Ce qui achève de démontrer que EFGH est un parallélogramme.
Remarques :
- EFGH est un rectangle si les diagonales de ABCD sont perpendiculaires.
- EFGH est un losange si les diagonales de ABCD sont de même longueur.
Aire du parallélogramme :
L’aire de EFGH est égale à la moitié de celle de ABCD.
Soit O le point d’intersection des diagonales de ABCD. On va démontrer que l’aire de OJEI est la moitié de celle de OBA. La parallèle à (BO) passant par E coupe (AO) en I. La parallèle!le à (AO) passant par E coupe (BO) en J. D’après le théorème de la droite des milieux, I et J sont les milieux respectifs des segments [AO] et [BO].
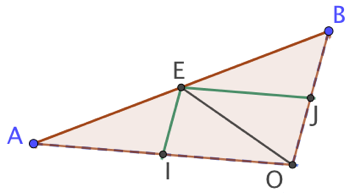Donc (EI) et (EJ) sont les médianes respectives de OEA et OBE. Or la médiane d’un triangle coupe celui-ci en deux triangles de même aire. Par conséquent les triangles EIA et EIO ont la même aire. De même les triangles EJO et EJB ont la même aire. Enfin, pour la même raison, les triangles EOA et EOB ont la même aire puisque E est le milieu de [AB].
Finalement les 4 triangles EIA, EIO, EJO et EJB ont la même aire. On en conclut que le parallélogramme l’aire de OJEI est la moitié de celle de OBA. Il suffit de reproduire le même raisonnement pour les triangles OAD, ODC et OCB pour achever la démonstration.
