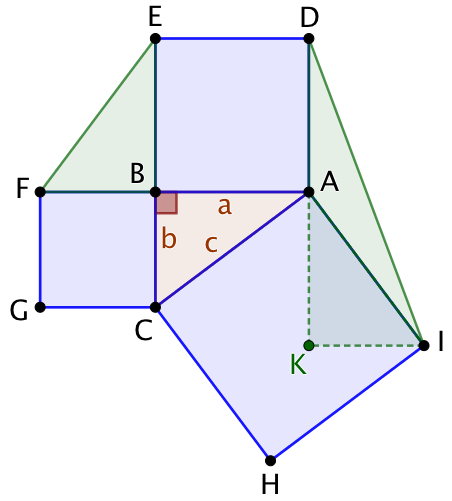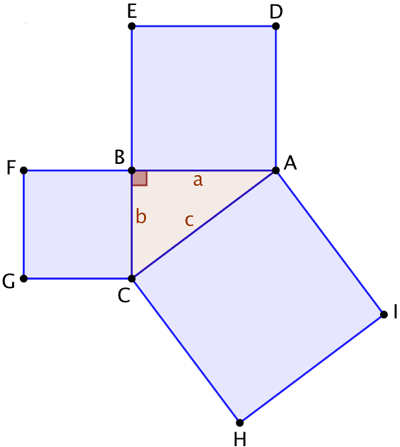
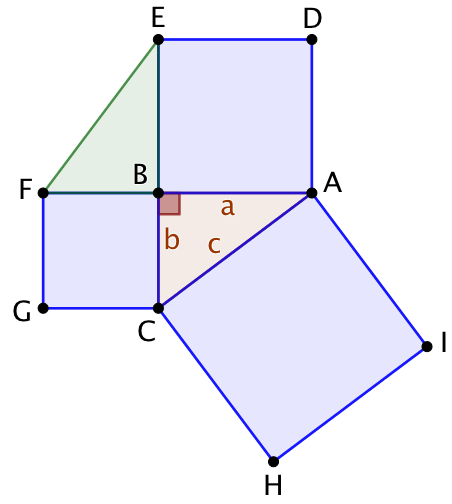
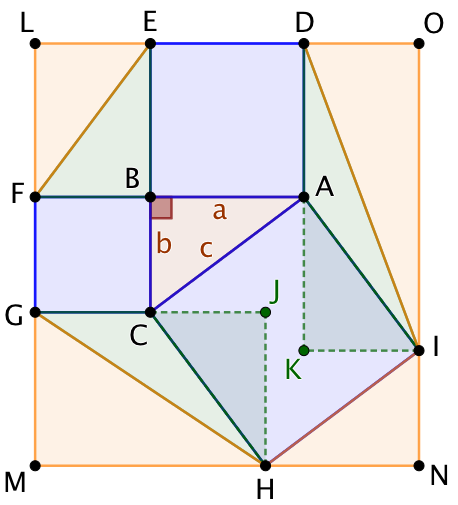
Théorème de Pythagore (par un grand rectangle)


L’objectif est de démontrer que l’aire du carré ACHI est égale à la somme des aires des carrés BFGC et BADE.	On complète par le triangle BEF isométrique au triangle ABC.	On complète par le triangle AID qui a la même aire que celle de ABC. Pour s’en convaincre il suffit d’appliquer une rotation de 90° à ABC qui l’envoie sur AKI. Ce qui permet de constater que [KI] est une hauteur de AID correspondant à la base [AD].
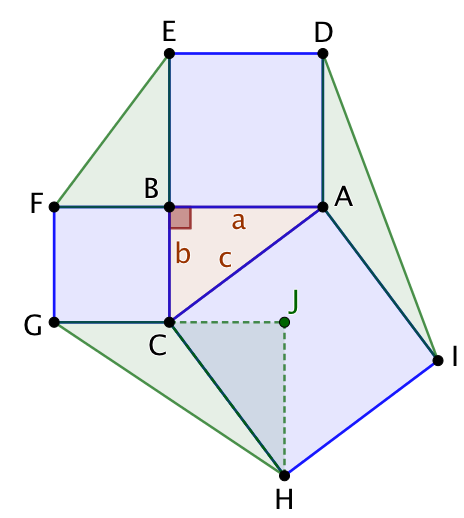
		Calcul direct : $LO = LE + ED + DO = b + a + b = a + 2b$ $LM = LF + FG + GM = a + b + a = 2a + b$ $LO \times LM = (a + 2b)(2a + b) = 2a^2 + 5ab + 2b^2$ Par découpages : LMNO est constitué des carrés ACHI, BFGC, BADE et de 1à triangles d’aire égale à celle de ABC, soit : $a^2 + b^2 + c^2 + 10\times \dfrac{ab}{2} = a^2 + b^2 + c^2 + 5ab$ On obtient donc l’égalité : $2a^2 + 5ab + 2b^2 = a^2 + b^2 + c^2 + 5ab$ , c’est-à-dire $a^2 + b^2 = c^2$ .
On complète par le triangle CGH qui a la même aire que celle de ABC. Pour s’en convaincre il suffit d’appliquer une rotation de 90° à ABC qui l’envoie sur CJH. Ce qui permet de constater que [HJ] est une hauteur de CGH correspondant à la base [CG].	On complète par 4 triangles pour obtenir un rectangle LMNO. FEL et HNI sont isométriques à ABC. Les aires de GMH et DOI sont double de celle de ABC. On va calculer l’aire du rectangle LMNO de deux manières.