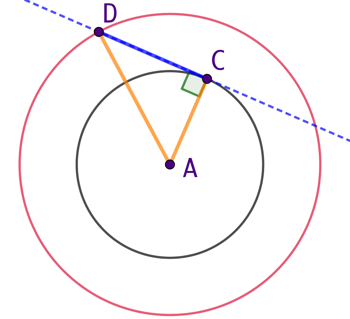
 Soit un cercle de centre A et un point C mobile sur ce cercle. Soit D un point de la tangente au cercle en C. Quand C parcourt le cercle et que la distance DC reste constante, le lieu géométrique décrit par D est un cercle de centre A.
Soit un cercle de centre A et un point C mobile sur ce cercle. Soit D un point de la tangente au cercle en C. Quand C parcourt le cercle et que la distance DC reste constante, le lieu géométrique décrit par D est un cercle de centre A.
Explications :
Le triangle ACD est rectangle en C donc ![]() . Or AC est un rayon du cercle donc de valeur constante. Par hypothèse CD est aussi constante, donc la distance AD est constante. Ce qui permet d’affirmer que D décrit un cercle de centre A.
. Or AC est un rayon du cercle donc de valeur constante. Par hypothèse CD est aussi constante, donc la distance AD est constante. Ce qui permet d’affirmer que D décrit un cercle de centre A.
