On veut démontrer que les symétriques de l’orthocentre d’un triangle appartiennent au cercle circonscrit à ce triangle.
Construction :
- On trace un triangle ABC quelconque.
- On place I le milieu de [BC]
- On place H orthocentre de ABC.
- On place O centre du cercle circonscrit à ABC.
- On place A’ symétrique de A par rapport à O.
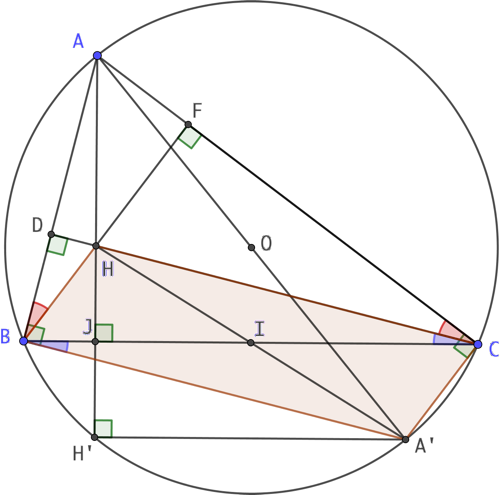Explications : On va démontrer que HCA’B est un parallélogramme en montrant que ses côtés opposés sont parallèles.
(CD) est la hauteur issue de C donc (CD) et (BA) sont perpendiculaires. Comme A’ est le symétrique de A par rapport à O, [AA’] est un diamètre du cercle circonscrit. Puisque B appartient à ce cercle, le triangle ABC est rectangle en B. Donc (A’B) est perpendiculaire à (BA). Conclusion (A’B) et (CD) sont parallèles et 
.
(BF) est la hauteur issue de B donc (BF) et (AC) sont perpendiculaires. On sait déjà que (CD) et (AB) sont perpendiculaires. Donc les triangles ABF et ADC sont semblables et par conséquent :
.
Puisque 
et , on en conclut que 
et que les (CA’) et (HB) sont parallèles. On vient de démontrer que HCA’B est un parallélogramme.
Puis que HCA’B est un parallélogramme, ses diagonales se coupent en leur milieu I. Par conséquent I est le milieu de [HA’]. Ce qui permet de conclure que le symétrique de H par le milieu de [BC] appartient au cercle circonscrit. On démontre de la même façon ce résultat pour les deux autres symétriques de H.
Remarque : on peut en déduire que H’, point d’intersection de (AH) et du cercle circonscrit, est le symétrique de H par rapport à (BC). On utilise le théorème des milieux dans le triangle HH’A’ : Le triangle AH’A’ est rectangle en H’ puisque [AA’] est un diamètre du cercle circonscrit à ABC et que H’ appartient à ce cercle. Par conséquent (H’A’) est perpendiculaire à (H’A) donc à (H’H). Or (BC) est perpendiculaire à (H’A) donc (HH’). Par conséquent (BC), c’est-à-dire (JI) est parallèle à (H’A’).
Dans le triangle HH’A’, (JI) et (H’A’) et I est le milieu de [HA’]. Donc J est le milieu de [HH’].
