Le symétrique d’une droite par rapport à un axe est une droite située de telle manière que l’axe soit la bissectrice intérieure de l’angle formé par ces deux droites.
Explications :
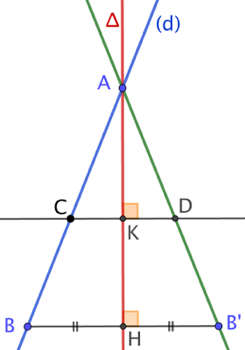
Soit un axe 
et une droite (d). On suppose que les deux droites sont sécantes en un point A. Soit B un autre point de (d) et B’ l’image de B par la symétrie d’axe . On va montrer que (AB’) est l’image de (d) par la symétrie d’axe .
Soit C un point, situé par exemple entre A et B, et (CD) la parallèle à (BB’) passant par C. Cette droite coupe au point K et (AB’) au point D. Vérifions à l’aide du théorème de Thales que que K est le milieu de [CD].
Soit H le milieu de [BB’].
Dans le triangle ABH : 
.
Dans le triangle AHB’ : 
.
Il vient alors que 
. Or BH = HB’. Par conséquent CK = KD.
Conclusion : l’image d’un point quelconque de (d) par rapport à est un point de (AB’). On démontre très facilement que est la bissectrice intérieure de l’angle 
puisqu’il est la médiatrice de [BB’].
Remarques :
- On vient de démontrer que l’image de (d) par la symétrie d’axe 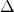est incluse dans (AB’). La rigueur mathématique imposerait de démontrer que l’image de (AB’) par la symétrie d’axe 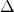est incluse dans (d); ce qui ne présente aucune difficulté.
- Il faudrait envisager le cas où C appartient à (d) sans appartenir à [AB]. La version “papillon” du théorème de Thales permet de traiter cela.
- Il faudrait aussi envisager le cas particulier où (d) et 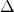sont deux droites parallèles. Démonstration très simple.
