Le symétrique axial d’un angle est un angle de même mesure dont le sommet est le symétrique axial de l’angle d’origine.
Explications :
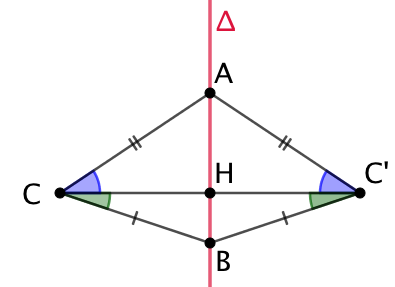
Soit un axe 
et l’angle 
, avec A et B sur . Soit C’ le symétrique axial de C. On sait que les symétriques axiaux respectifs des segments [CA] et [CB] sont [C’A] et [C’B].
Soit H le point d’intersection de (CC’) et de . Comme est la médiatrice de [CC’], les triangles CAC’ et CBC’ sont isocèles de base commune [CC’]. Leurs angles à la base ont la même mesure :
et 
.
or 
et 
.
On en conclut que 
.
