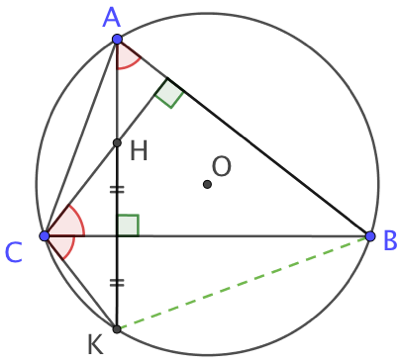
Les symétriques de l’orthocentre par rapport aux côtés du triangles appartiennent au cercle circonscrit au triangle.
Soit H l’orthocentre du triangle ABC. On trace le cercle circonscrit à ABC (de centre O). La hauteur AH coupe ce cercle au point K qui est le symétrique de H par rapport à (BC).
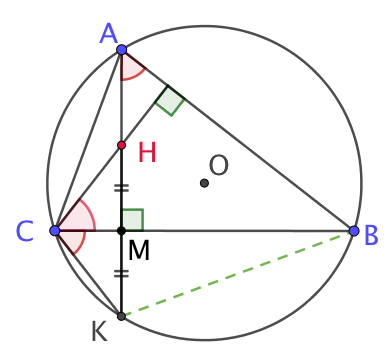 Explications :
Explications :
On va montrer que les triangles CKM et CHM sont isométriques. Pour cela il suffit de vérifier que ![]() .
.
![]() car ces deux angles interceptent le même arc de cercle KB.
car ces deux angles interceptent le même arc de cercle KB.
![]() car ses deux angles ont des côtés deux à deux perpendiculaires.
car ses deux angles ont des côtés deux à deux perpendiculaires.
Or ![]()
Donc ![]() .
.
Par conséquent les triangles CKM et CHM ont deux angles de mêmes mesures deux à deux et un côté commun CM entre ces deux angles. Ils sont donc isométriques. Alors HM = MK. Ce qui achève de démontrer que H et K sont symétriques par rapport à (BC).