Symétrie axiale

I – Figures symétriques

Définitions
Deux figures sont symétriques par rapport à une droite si elles se superposent par pliage le long de cette droite. Cette droite est appelée l’axe de symétrie.

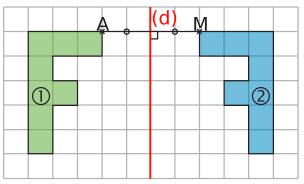
Exemple : Les figures 1 et 2 se superposent par pliage le long de la droite (d) donc elles sont symétriques par rapport à la droite (d).

On dit également que la figure 1 est le symétrique de la figure 2 dans la symétrie axiale d’axe (d).

II – Symétrique d’un point

Définition
Le symétrique d’un point A par rapport à une droite (d) est le point M tel que la droite (d) soit la médiatrice du segment [AM], c’est-à-dire tel que (d) soit la perpendiculaire au segment [AM] et passe par son milieu.

Exemple : Dans la figure ci-dessus, les points A et M sont symétriques par rapport à la droite (d).

Remarque : Si un point appartient à une droite alors son symétrique par rapport à cette droite est le point lui-même.

Construction du symétrique d’un point par rapport à une droite.

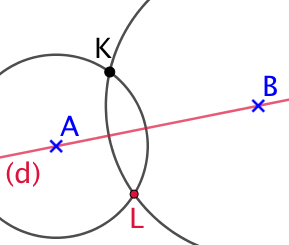Objectif : On veut placer le point L, symétrique du point K par rapport à la droite (d), en utilisant uniquement un compas.

Voici les étapes de la construction :

  1. On choisit deux points A et B sur la droite (d).
  2. On trace le cercle de centre A qui passe par K.
  3. On trace le cercle de centre B qui passe par L.
  4. Les deux cercles se croisent évidemment en K mais aussi en un nouveau point qui est le point L, symétrique de K par rapport  (d).

III – Symétrique de figures usuelles et propriétés de la symétrie axiale

 

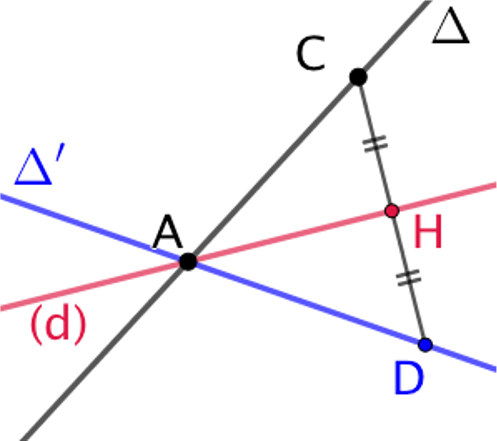
Propriétés admises. On pourra les vérifier à l'aide de Géogébra.
  • Le symétrique d’une droite par rapport à un axe est une droite. La symétrie axiale conserve l’alignement.
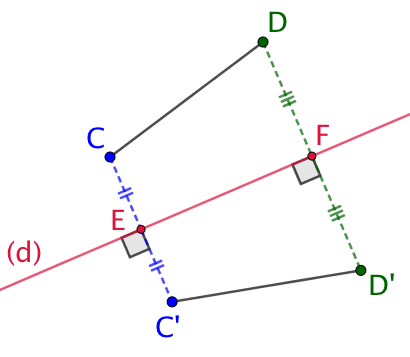
  • Le symétrique d’un segment par rapport à un axe est un segment de même longueur. La symétrie axiale conserve les longueurs.
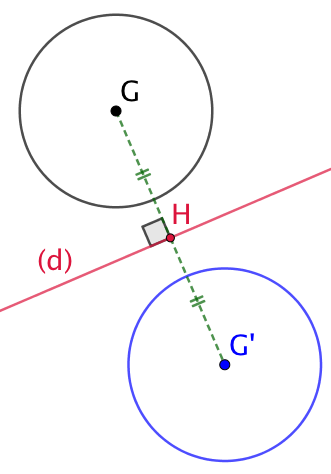
  • Le symétrique d’un cercle par rapport à un axe est un cercle de même rayon. Les centres des cercles sont symétriques par rapport à cet axe.
  • La symétrie axiale conserve les mesures des angles, les périmètres et les aires.
Symétrie axiale d’une droite \Delta par rapport à l’axe (d) Symétrie axiale d’un segment [CD] par rapport à l’axe (d) Symétrie axiale d’un cercle de centre G par rapport à l’axe (d)
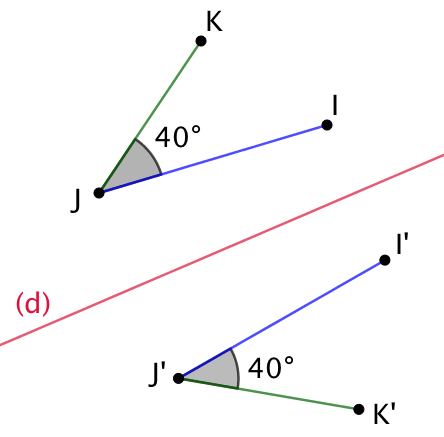Symétrie axiale d’un angle \widehat{IJK} par rapport à l’axe (d)
Méthode
Pour construire le symétrique d’une figure complexe, on la décompose en figures usuelles et on construit le symétrique de chacune d’elles.

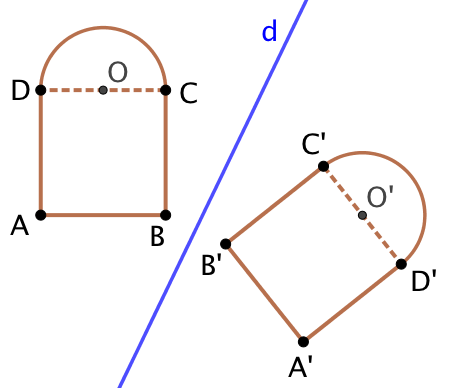Exemple : Voici une figure ABCD composée d’un carré et d’un demi cercle de centre O.

Voici les étapes de construction de son symétrique par rapport à la droite d.

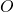  1. On construit les symétriques des 5 points : A, B, C, D et O par rapport à 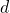d. On obtient les points 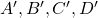A', B', C', D' et O'
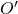
  2. On trace les segments [A'B'], [B'C'], [C'D'] et [D'A'].
  3. On trace au compas le demi cercle de centre 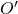O' et passant par les points 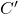C' et D'.

 

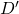IV – Axe de symétrie d’une figure

Définition
Une droite (d) est un axe de symétrie d’une figure si les deux parties de la figure se superposent par pliage le long de cette droite.

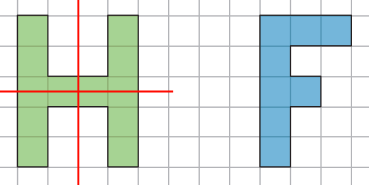Exemple :

La figure H admet deux axes de symétrie (tracés en rouge) tandis que la figure F n’en a aucun.

V – Axes de symétrie des figures usuelles

Propriétés
  • Un segment a deux axes de symétrie : la droite qui contient ce segment et la médiatrice de ce segment.
  • Si un point appartient à la médiatrice d’un segment, alors il est situé à égale distance des extrémités de ce segment.
  • Réciproquement, si un point est équidistant des extrémités d’un segment, alors il appartient à la médiatrice de ce segment.

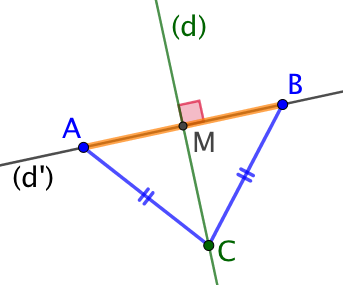Exemple :

A et B sont deux points de la droite (d’).

Le segment [AB] a deux axes de symétries : sa médiatrice (d) et la droite (d’) qui est en fait la droite [AB].

 

Propriété
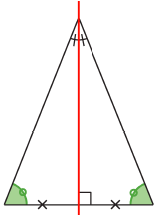  • Un triangle isocèle a un axe de symétrie qui est la médiatrice de sa base.
  • Conséquence : Dans un triangle isocèle, les angles à la base ont la même mesure.

Explication : Par pliage selon a médiatrice de sa base, un des deux angles verts va recouvrir exactement l’autre angle vert.

Propriété

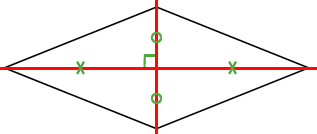
  • Un losange a deux axes de symétrie qui sont ses diagonales.
  • Conséquence : Dans un losange, les diagonales se coupent en leur milieu et sont perpendiculaires.

Explication : Un losange peut se décomposer en deux triangles isocèles. Les diagonales du losange sont les médiatrices des triangles isocèles.

Propriété

  • Un triangle équilatéral a trois axes de symétrie qui les médiatrices de ses côtés et les bissectrices de ses angles.
  • Conséquence : Dans un triangle équilatéral, tous les angles ont la même mesure (60°).

Explication : Un triangle équilatéral est pour chacun de ses sommets un triangle isocèle.

Propriété

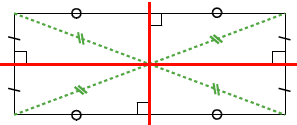
  • Un rectangle a deux axes de symétrie qui sont les médiatrices de ses côtés.
  • Conséquence :Dans un rectangle, les diagonales se coupent en leur milieu et ont la même longueur.

Explication : un rectangle peut se découper en quatre triangles isocèles.

Propriété

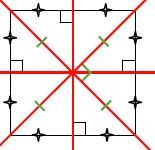
  • Un carré a quatre axes de symétrie qui sont les médiatrices de ses côtés et ses diagonales.
  • Conséquence : Dans un carré, les diagonales se coupent en leur milieu, sont perpendiculaires et ont la même longueur.

Explication : Un carré est à la fois un losange et un rectangle.

 

Print Friendly, PDF & Email