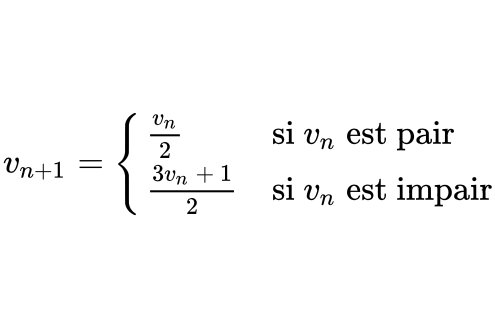Monotonies
![]()
Suites arithmétiques
![Rendered by QuickLaTeX.com \[ u_n = u_p + (n-p)r \qquad \qquad \sum_{k=p}^n u_k = (n-p+1) \dfrac{u_p + u_n}{2} \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-9e276e61e64030fe9a34b508e6a83f4a_l3.png)
Suites géométriques
![]()
Autres suites
Suites arithmético-géométriques : On étudie le point fixe de sa fonction affine associée.
Suite définie par des récurrences linéaires d’ordre 2 : Pour calculer explicitement son terme général, on étudie les solutions de son équation caractéristique. Cela ressemble aux équations différentielles d’ordre 2. Les deux constantes sont déterminées par les deux premiers termes de la suite.
CONVERGENCE
Soit ![]() une suite positive et
une suite positive et ![]() . Si à partir d’un certain rang,
. Si à partir d’un certain rang, ![]() alors la suite converge vers 0.
alors la suite converge vers 0.
- Toute suite convergente est bornée.
- Toute suite croissante (resp. décroissante) et majorée (resp. minorée) est convergente.
- Toute suite croissante (resp. décroissante) et non majorée (resp. minorée) a une limite infinie.
Soit ![]() et soient
et soient ![]() tels que
tels que ![]() alors à partir d’un certain rang,
alors à partir d’un certain rang, ![]() .
.
Soit ![]() . Alors
. Alors ![]() est du signe de
est du signe de ![]() à partir d’un certain rang.
à partir d’un certain rang.
![]() et
et ![]() minorée, alors
minorée, alors ![]() .
.
![]() et
et ![]() minorée par un nombre strictement positif, alors
minorée par un nombre strictement positif, alors ![]() .
.
Soient ![]()
![]()
Cas particulier du théorème des gendarmes : S’il existe ![]() convergente vers 0 telle que
convergente vers 0 telle que ![]() alors
alors ![]() converge vers 0.
converge vers 0.
Suites adjacentes : Soient une suite ![]() croissante et une suite
croissante et une suite ![]() décroissante tel que
décroissante tel que ![]() , alors ces deux suites convergent vers la même limite
, alors ces deux suites convergent vers la même limite ![]() telle que
telle que ![]() .
.
Théorème de Bolzano-Weierstrass : De toute suite réelle bornée on peut extraire une sous-suite convergente.
Conséquence : Pour montrer qu’une suite diverge, il suffit de trouver deux suites extraites qui n’admettent pas la même limite.
Suite de Cauchy : ![]() tel que
tel que ![]()
Toute suite de Cauchy est bornée. Toute suite de Cauchy dans \mathbb{R} est convergente.
Suite définie par une fonction : 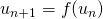
- Si
 est continue et si
est continue et si 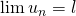 alors
alors 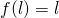 .
. - Si
 croissante alors
croissante alors 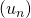 monotone et son sens de variation est donné par le signe de
monotone et son sens de variation est donné par le signe de 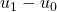 .
. 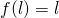 . Si
. Si 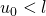 alors la suite
alors la suite 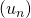 est majorée par
est majorée par 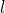 ; sinon elle est minorée.
; sinon elle est minorée.- Si
 est décroissante alors
est décroissante alors 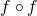 est croissante. Les suites
est croissante. Les suites 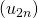 et
et 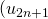 sont monotone et de sens de variation contraire.
sont monotone et de sens de variation contraire.
Suite complexe
![]() suites réelles.
suites réelles.
![]() converge si et seulement si
converge si et seulement si ![]() et
et ![]() convergent et dans ce cas :
convergent et dans ce cas : ![]() .
.
NOTATIONS DE LANDAU
![]()
![]()
![]()
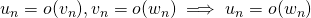
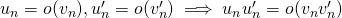
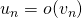 et si les deux suites ne s’annulent plus à partir d’un certain rang, alors
et si les deux suites ne s’annulent plus à partir d’un certain rang, alors 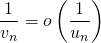
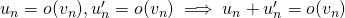
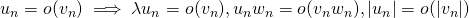
- Propriétés identiques pour O (domination)
 est une relation d’équivalence dans l’ensemble des suites
est une relation d’équivalence dans l’ensemble des suites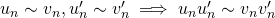
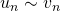 et si les deux suites ne s’annulent plus à partir d’un certain rang, alors
et si les deux suites ne s’annulent plus à partir d’un certain rang, alors 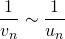
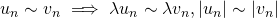
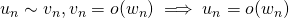
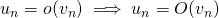
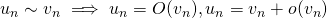
Deux suites équivalentes sont de même nature. Si elles ne s’annulent pas à partir d’un certain rang, elles sont de même signe. Si l’une converge, l’autre converge vers la même limite.