Suites introduction

I. RAPPELS

Calculer avec des pourcentages
Règle n°1 : Augmenter une valeur de t % revient à la multiplier par 1+\dfrac{t}{100}.

Règle n°2 : Diminuer une valeur de t % revient à la multiplier par 1-\dfrac{t}{100}.

Exemples :
En début d’année, l’effectif d’une entreprise était de 140 personnes. En fin d’année, on note une croissante de 8% de cet effectif. L’effectif en fin d’année est : 140 \times (1 + \dfrac{8}{100}) = 140 \times 1,08 \approx 151.

Pendant les soldes, le gérant d’un magasin de vêtements décide de baisser ses prix de 20%. Le nouveau tarif d’un pantalon qui valait 85 € avant les soldes est : 85 \times (1 - \dfrac{20}{100}) = 85 \times 0,8 = 68 €.

II. MODE DE GÉNÉRATION D’UNE SUITE NUMÉRIQUE

Définition d’une suite numérique
Une suite numérique (u_n) est une fonction de ℕ dans ℝ qui à tout entier naturel n associe son image u(n) que l’on a l’habitude de noter u_n.

u_n est le terme de rang n et n est son indice.

Vocabulaire et notation

Le terme initial de la suite (u_n) est

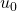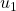  • u_0 si la numérotation commence à partir de 0
  • u_1 si la numérotation commence à partir de 1
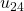  • u_{24} si la numérotation commence à partir de 24

Le terme suivant de u_n est u_{n+1}

Le terme précédent de u_n  est u_{n-1}

Suite définie par une formule explicite
Une suite numérique  (u_n)  est définie de manière explicite s’il existe une fonction f telle que pour tout entier naturel  n , u_n=f(n).

Exemple : La suite (u_n) est définie par u_n=3n+1, pour tout entier naturel n

Alors u_0=3 \times 0+1=1 \qquad \qquad u_1=3 \times 1+1=4 \qquad \qquad u_2=3 \times 2+1=7

Suite définie par une relation de récurrence
Une suite numérique  (u_n) est définie par récurrence si on connait son premier terme et la relation permettant de calculer chaque terme à partir du terme précédent.

Exemple : La suite (u_n) est définie par u_0=3 et pour tout entier naturel n, u_{n+1} = 2u_n+5

La relation de récurrence est n, u_{n+1} = 2u_n+5. Le premier terme est u_0=3.

Alors u_1 = 2 \times u_0 + 5 = 2 \times 3 + 5 = 11 et u_2 = 2 \times u_1 + 5 = 2 \times 11 + 5 = 27

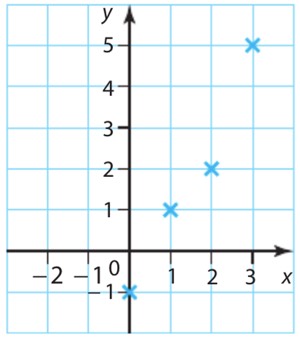
III. REPRÉSENTATION GRAPHIQUE D’UNE SUITE

Définition
Dans un plan rapporté à un repère, une représentation des termes de la suite (u_n) est l’ensemble des points de coordonnées (n,u_n) avec n entier naturel. On obtient un nuage de points.

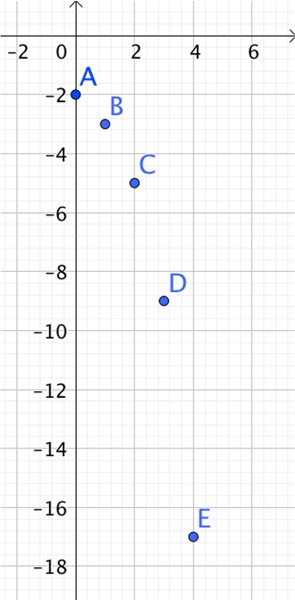Exemple : la suite (u_n) est définie pour tout entier naturel n par u_0 = -2 et u_{n+1} = 2u_n + 1

u_1 = -3 \qquad u_2 = -5 \qquad u_3 = -9 \qquad u_4 = -17

On va placer dans le repère les points A(0,u_0), B(1,u_1), C(2,u_2), D(3,u_3), E(4,u_4), ...

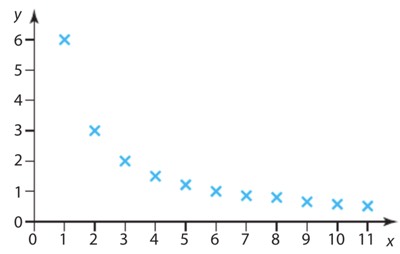
IV. SENS DE VARIATION

Définition
Une suite (u_n) est croissante lorsque, pour tout n, u_n \le u_{n+1}

Une suite (u_n) est décroissante lorsque, pour tout n, u_n \ge u_{n+1}

Suite croissante Suite décroissante
Étude du sens de variation d’une suite par le calcul
Il suffit de déterminer le signe de u_{n+1} - u_n.

  • Si cette différence est positive pour tout 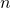n, alors la suite est croissante.
  • Si cette différence est négative pour tout 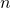n, alors la suite est décroissante
Print Friendly, PDF & Email