Statistiques

I – Série statistique

Définition
Une série statistique est le résultat d’une enquête réalisée sur une population d’individus (groupe de personnes ou d’objets), pour lesquels on mesure la présence d’un certain caractère.

Exemples :

  • La taille des élèves d’une classe,
  • Le nombre de but marqués par une équipe de football et par match au cours, d’une année,
  • Le nombre de voyageurs qui utilisent chaque jour le métro.

Exemple utilisé dans la première partie du cours : liste des mois de naissance de 50 élèves de 5ème d’un collège :

  • mars    janv.    avril    sept.    févr.    nov.     mai      nov.     juill.    avril
  • juin      sept.    oct.      nov.     mai      déc.     déc.     mai      août     nov.
  • juill.    avril    juill.    janv.    avril     nov.     mars    août     juin      juill.
  • avril    août     mars    nov.     juill.    nov.     avril    janv.    déc.     mai
  • mai      févr.    juill.    sept.    avril    déc.     sept.    mai      oct.      juin

La population étudiée est le groupe des élèves de cinquième. Chaque individu est un élève. Le caractère étudié est le mois de naissance de chaque individu. Les valeurs prises par le caractères sont les 12 mois de l’année.

Définitions
  • L’effectif d’une valeur est le nombre de fois où cette valeur apparaît dans la série statistique.
  • L’effectif total est le nombre de valeurs dans la série statistique.

Exemples :

L’effectif de la valeur « Mars » est le nombre d’élèves nés en mars. Il faut compter dans la liste des mois de naissance le nombre de fois où apparaît « Mars ». On obtient : 3

L’effectif de la valeur « Juillet » est : 6

L’effectif total de la série est 50.

Définition
Le tableau d’effectifs permet de regrouper les effectifs de toutes les valeurs d’une série statistique.

Le tableau des effectifs pour la série statistiques des mois de naissances des élèves de cinquième est le suivant :

Pour connaître le nombre d’enfants nés en septembre, on lit le nombre inscrit dans la case sous celle du mois de septembre. On lit : 4.

On remarque qu’en faisant la somme de tous les effectifs, on retrouve le nombre : 50, qui est le nombre d’individus de la série statistique.

Définition
  • La fréquence d’une valeur est le quotient : \dfrac{\text{effectif de la valeur}}{\text{effectif total}}.
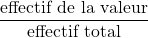  • Une fréquence peut être exprimée sous une forme décimale, par une fraction ou par un pourcentage.

Exemple : La fréquence de la valeur « Avril » de la série statistique des mois de naissances est : \dfrac{7}{50} = 0,14 = 14\%.

On calcule toutes les fréquences pour obtenir le tableau suivant :

Propriété
La somme de toutes fréquences d’une série statistique est toujours égale à 1, c’est-à-dire 100%.

II – Moyenne

Une entreprise possède 30 ordinateurs, numérotés de 1 à 30. Elle réalise un tableau donnant l’âge de chacun de ses ordinateurs et qui est une série statistique :

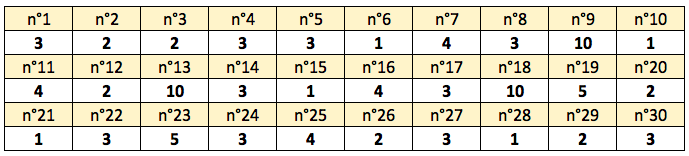
Elle établit ensuite le tableau des effectifs et des fréquences de cette série statistique :

Âge 1 2 3 4 5 10
Effectif 5 6 10 4 2 3
Fréquence \dfrac{5}{30} 0,2 \dfrac{1}{3} \dfrac{2}{15} \dfrac{1}{15} \dfrac{1}{10}

 

Définition
La moyenne d’une série statistique est égale à la somme de toutes les valeurs divisée par l’effectif total.

Exemple : On reprend la série statistiques sur l’âge des ordinateurs,

  • L’effectif total est 30 puisqu’il y a 30 ordinateurs dans l’entreprise.
  • La somme de toutes les valeurs est la somme de tous les âges de tous les ordinateurs, soit 108

La moyenne de cette série statistique est : \dfrac{108}{30} = 3,6. Cela signifie que l’âge moyen des ordinateurs est de 3,6 ans.

III – Représentation graphique

1) Diagramme en bâtons

Définition
Dans un diagramme en bâtons, les hauteurs des bâtons sont proportionnelles aux quantités représentées.

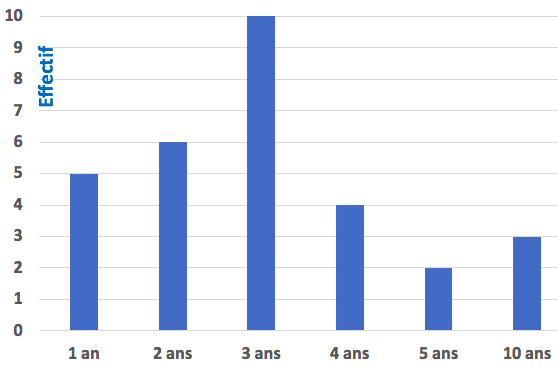Exemple : âge des ordinateurs de l’entreprise.

Ce diagramme donne les mêmes informations que le tableau des effectifs de la série statistique

2) Diagramme circulaire (camembert)

Définition
Dans un diagramme circulaire, les mesures des angles sont proportionnelles aux quantités représentées.

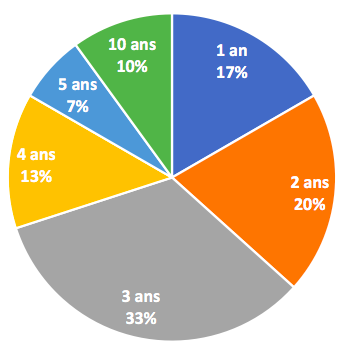Exemple : âge des ordinateurs de l’entreprise.

Ce diagramme donne les mêmes informations que le tableau des fréquences de la série statistique.

Les fréquences sont données en pourcentages et sont arrondies au centième.

Print Friendly, PDF & Email