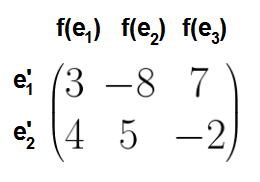![Rendered by QuickLaTeX.com \[ B_E = (e_1,e_2,\dots,e_p) \qquad B_F=(f_1,f_2,\dots,f_n) \qquad \phi \in L(E,F) \qquad \phi(e_j) = \sum_{i=1}^n a_{ij} f_i \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-e39e8e451d69756323ff8b13df56bdf2_l3.png)
La matrice de ![]() dans les bases
dans les bases ![]() et
et ![]() est
est ![]() et est notée
et est notée ![]() . La jème colonne
. La jème colonne ![]() donne les coordonnées de
donne les coordonnées de ![]() dans la base
dans la base ![]() . Le nombre de colonnes est donné par la dimension de l’espace de départ, et le nombre de lignes par celle de l’espace d’arrivée.
. Le nombre de colonnes est donné par la dimension de l’espace de départ, et le nombre de lignes par celle de l’espace d’arrivée.
![]() définie par
définie par ![]() est un isomorphisme d’espace vectoriel. Donc dim
est un isomorphisme d’espace vectoriel. Donc dim ![]() .
.
![]() triangulaire supérieure si et seulement si
triangulaire supérieure si et seulement si ![]() . C’est-à-dire si et seulement si
. C’est-à-dire si et seulement si ![]() est stable par
est stable par ![]() .
.
Soit ![]() :
:
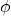 projecteur si et seulement si
projecteur si et seulement si 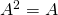
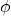 symétrie si et seulement si
symétrie si et seulement si 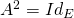
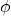 nilpotent si et seulement si
nilpotent si et seulement si 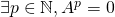
Soit ![]() .
. ![]() inversible si et seulement si
inversible si et seulement si ![]() est inversible. De plus
est inversible. De plus ![]()
Soit ![]() est une base de
est une base de ![]() si et seulement si
si et seulement si ![]() est inversible.
est inversible.
Soit ![]() et
et ![]() une application linéaire associée à
une application linéaire associée à ![]() :
:
- Ker
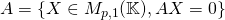 , SEV de
, SEV de 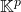 . C’est l’ensemble des solutions de l’équation
. C’est l’ensemble des solutions de l’équation 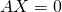 .
. - Im
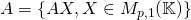 , SEV de
, SEV de 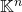 engendré par les colonnes de
engendré par les colonnes de 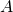 .
. 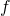 injective si et seulement si Ker
injective si et seulement si Ker 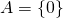
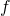 surjective si et seulement si Im
surjective si et seulement si Im 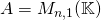
Matrice de passage
![]() est la matrice représentative de l’application identité
est la matrice représentative de l’application identité ![]() , de
, de ![]() muni de la base
muni de la base ![]() dans
dans ![]() muni de la base
muni de la base ![]() .
.
![Rendered by QuickLaTeX.com \[ X = \left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right) \text{ et } X' = \left( \begin{array}{c} x_1' \\ x_2' \\ \vdots \\ x_n' \end{array} \right) \text{ coordonn\'ees de } x \text{ dans les bases } B \text{ et } B' \longrightarrow X = P_{BB'} X' \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-5e6304ae2090cf0b2d6fbd6fb1e9b751_l3.png)
Double changement de base pour une application linéaire
![]()
![]()
Application linéaire canoniquement associée
Soit ![]() . L’application linéaire canoniquement associée à
. L’application linéaire canoniquement associée à ![]() est
est ![]() de
de ![]() vers
vers ![]() dont une matrice associée est
dont une matrice associée est ![]() .
.
Rang de A :
- rg
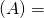 rg
rg 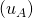 . C’est le rang de la famille de ses vecteurs colonne.
. C’est le rang de la famille de ses vecteurs colonne. - rg
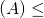 inf
inf 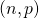
- dim Ker
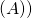 + rg
+ rg 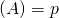
Matrice canonique d’une application linéaire
Soient dim ![]() , dim
, dim ![]() et
et ![]() de rang
de rang ![]() .
.
Alors il existe une base de ![]() et une base de
et une base de ![]() telles que la matrice de
telles que la matrice de ![]() sur ces deux bases soit, en l’écrivant par blocs :
sur ces deux bases soit, en l’écrivant par blocs :
![]()
MATRICES SEMBLABLES
Deux matrices carrées ![]() et
et ![]() sont semblables s’il existe une matrice inversible
sont semblables s’il existe une matrice inversible ![]() telle que
telle que ![]() .
.
Deux matrices carrées ![]() et
et ![]() sont semblables si elles représentent le même endomorphismes pour deux bases différentes.
sont semblables si elles représentent le même endomorphismes pour deux bases différentes.
Deux matrices semblables ont le même déterminant.
Soient ![]() et
et ![]() deux matrices semblables et
deux matrices semblables et ![]() , les matrices
, les matrices ![]() et
et ![]() sont semblables.
sont semblables.