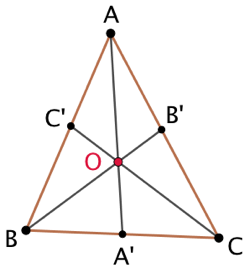
Relation de Gergonne – Un peu de mathématiques

Soient un triangle ABC et un point O dans ABC. (AO), (BO) et (CO) coupent les trois côtés de ABC aux points A’, B’ et C’. Alors : $\dfrac{OA'}{AA'} + \dfrac{OB'}{BB'} + \dfrac{OC'}{CC'} = 1$ .

Explications :

En appliquant 3 fois le lemme du Chevron sur ABC :

$\dfrac{Aire_{OBC}}{Aire_{ABC}} = \dfrac{OA}{AA'} \qquad \qquad \dfrac{Aire_{OCA}}{Aire_{ABC}} = \dfrac{OB'}{BB'} \qquad \qquad \dfrac{Aire_{OAB}}{Aire_{ABC}} = \dfrac{OC'}{CC'}$

En additionnant membre à membre ces 3 égalités, on obtient : $\dfrac{Aire_{OBC}+Aire_{OAC}+Aire_{OAB}}{ABC} = \dfrac{OA}{AA'} + \dfrac{OB}{BB'} + \dfrac{OC'}{CC'}$

$Aire_{OBC}+Aire_{OAC}+Aire_{OAB} = Aire_{ABC}$ . Ce qui permet de conclure que $\dfrac{OA'}{AA'} + \dfrac{OB'}{BB'} + \dfrac{OC'}{CC'} = 1$ .