 Étant donné le triangle ABC, on construit le cercle inscrit ainsi :
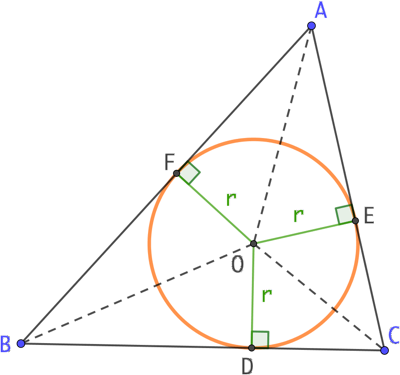
Étant donné le triangle ABC, on construit le cercle inscrit ainsi :
- On trace deux bissectrices, par exemple celles issues de A et de B, qui se coupent au point O. (La figure inclut la 3ème bissectrice mais ce n’est pas nécessaire).
- On réalise la projection orthogonale de O sur l’un des côtés du triangle, par exemple D.
- Le cercle inscrit est le cercle de centre O passant par D.
Le rayon du cercle inscrit est égal à deux fois l’aire du triangle divisée par son périmètre : ![]()
Explications :
On complète la figure avec les points E et F, projections orthogonales de O sur (AC) et (AB). Comme (OA) est la bissectrice de l’angle ![]() , on peut affirmer que
, on peut affirmer que ![]() . On montre de la même façon que
. On montre de la même façon que ![]() . Notons
. Notons ![]() .
.
Soient S l’aire du triangle ABC et P son périmètre. S est la somme des aires des six triangles rectangles formant ABC. Par exemple, l’aire du triangle AFO est ![]() .
.
Alors ![]() . Ce qui donne bien
. Ce qui donne bien ![]() .
.
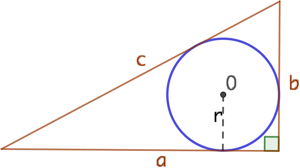 Cas particuliers :
Cas particuliers :
Si le triangle est rectangle avec des côtés de longueurs a, b et c, alors ![]() et
et ![]() , soit
, soit ![]() .
.
On montre facilement que ![]() . Or le triangle étant rectangle, nous avons l’égalité :
. Or le triangle étant rectangle, nous avons l’égalité : ![]() . Par conséquent
. Par conséquent ![]() donc
donc ![]() . Conclusion
. Conclusion ![]() .
.
Si on considère le fameux triangle (rectangle) de Pythagore pour lequel a = 3, b = 4 et c = 5, le rayon du cercle inscrit vaut donc la moitié de 3 + 4 – 5, soit 1.
