 Etant donné un triangle quelconque ABC, on construit un triangle DEF dont l’aire est quatre fois celle de ABC.
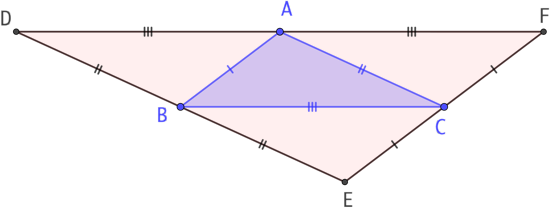
Etant donné un triangle quelconque ABC, on construit un triangle DEF dont l’aire est quatre fois celle de ABC.
Pour cela il suffit de tracer les parallèles aux trois côtés passant par les trois sommets opposés de ABC. Par exemple, la droite (DE) est la parallèle à (AC) qui passe par B.
Explications :
Observons le quadrilatère ABCF : par construction (EF) est parallèle à (AB) et (DF) est parallèle à (BC). Donc ABCF est un parallèlogramme. Ce qui conduit aux deux égalités de distance : AB = CF et AF = BC.
On démontrerait de la même manière que AD = BC, DB = AC, BE = AC et AB = EC. Par conséquent les triangles ABD, ACF et BCE sont isométriques avec ABC et ces quatre triangles ont la même aire. L’aire de DEF est bien égale au quadruple de celle de ABC.
 Curiosité :
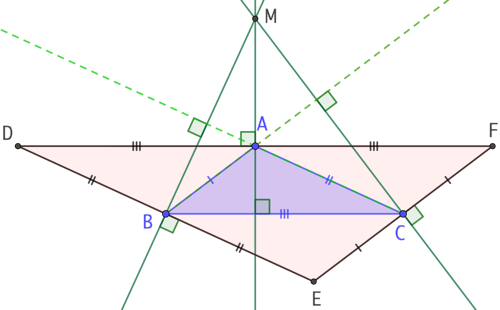
Curiosité :
On trace les trois hauteurs (AM), (BM) et (CM) de ABC. On note que celles-ci sont les trois médiatrices du triangle DEF.
Par exemple, considérons la hauteur (AM). Par définition (AM) est perpendiculaire à (BC). Or (BC) est parallèle (DF). Donc (AM) est aussi perpendiculaire à (DF). On a démontré que DA = AF, donc A est le milieu du segment [DF]. On peut alors conclure que (AM) est la médiatrice de [DF].
