On veut construire un quadrilatère inscriptible pour lequel on nous donne la mesure d’un angle 
, la longueur d’un côté adjacent 
et les longueurs des deux diagonales 
et 
.
 |
 |
 |
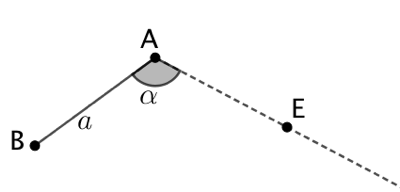
On place le sommet A et on trace le côté [AB] tel que  . On trace une demi-droite [AE) tel que  . |
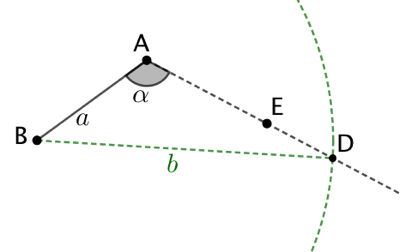
Première diagonale : On trace un cercle de centre B et de rayon qui coupe [AE) au point D. |
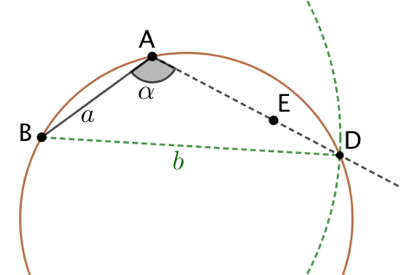
Puisque le quadrilatère est inscriptible, on trace le cercle passant par B, A et D. |
 |
 |
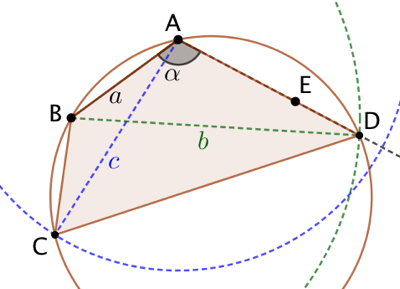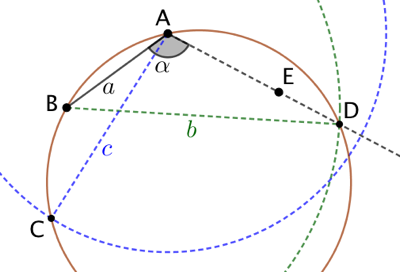
Seconde diagonale : On trace un cercle de centre A et de rayon . Il coupe le cercle BAD en C, qui est le quatrième sommet du quadrilatère recherché. |
Conditions d’existence du quadrilatère : Il faut que soit inférieur au diamètre du cercle BAD.
