Cas particuliers : ![]() et
et ![]()
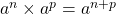
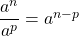 , avec
, avec 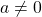
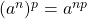
Exemples :
Démonstrations :
![]()
![]() d’après la propriété précédente.
d’après la propriété précédente.
![]()
Démonstrations :
D’une part ![]() et d’autre part, d’après une propriété précédente :
et d’autre part, d’après une propriété précédente : ![]() . Par conséquent
. Par conséquent ![]() .
.
D’une part ![]() et d’autre part, d’après une propriété précédente :
et d’autre part, d’après une propriété précédente : ![]() . Par conséquent
. Par conséquent ![]() .
.
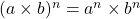
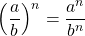 , avec
, avec 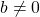
Exemples :
Démonstrations :
![]()
![]()
Exemples :
- Distance moyenne Terre – Soleil en km :
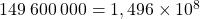
- Diamètre maximal du virus SARS-CoV-2 en mm :
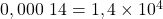
Ordre de grandeur : La notation scientifique permet de trouver immédiatement l’ordre de grandeur d’un nombre.
Une année-lumière = ![]() m. L’ordre de grandeur de l’année lumière est :
m. L’ordre de grandeur de l’année lumière est : ![]() m
m
EXERCICES
Exercice n°1 : Écrire les nombres suivants sous la forme ![]() , où
, où ![]() et
et ![]() sont des entiers relatifs.
sont des entiers relatifs.
![]()
Exercice n°2 : Écrire les nombres suivants sous la forme ![]() , où
, où ![]() est un entier relatif.
est un entier relatif.
![]()
Exercice n°3 : Écrire les expressions suivantes sous la forme ![]() où
où ![]() et
et ![]() sont des réels non nuls et où
sont des réels non nuls et où ![]() et
et ![]() sont des entiers relatifs.
sont des entiers relatifs.
![]()
Exercice n°4 :
- Calculer
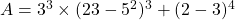
- Donner l’écriture scientifique de
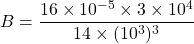
Exercice n°5 : Parmi les calculs suivants, lesquels ont pour résultat ![]()
![]()
Exercice n°6 : Écrire les nombres suivants sous la forme ![]() , où
, où ![]() est un entier relatif.
est un entier relatif.
![]()
Exercice n°7 :
- Le nombre
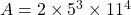 est-il multiple de
est-il multiple de 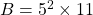
- Les nombres
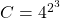 et
et 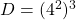 sont-ils égaux ?
sont-ils égaux ?
Exercice n°8 : Donner l’écriture scientifique des nombres suivant :
![]()
Exercice n°9 : Écrire A et B sous la forme ![]() , où
, où ![]() est un réel non nul et
est un réel non nul et ![]() est un entier relatif.
est un entier relatif.
![]()
Exercice n°10 : Écrire C, D, E et F sous la forme ![]() où
où ![]() et
et ![]() sont des réels non nuls et
sont des réels non nuls et ![]() et
et ![]() sont des entiers relatifs
sont des entiers relatifs
![]()
Exercice n°11 : Écrire A, B et C sous la forme ![]() où
où ![]() est un entier relatif.
est un entier relatif.
![]()
Exercice n°12 : La lune tourne autour de la Terre selon une orbite elliptique. La distance moyenne Terre-Lune est environ 384 400 km. On dispose d’une très (très) grande feuille de papier de 0,1 mm d’épaisseur. On plie cette feuille plusieurs fois sur elle-même et on admet qu’il est physiquement possible d’effectuer ces pliages autant de fois que souhaité. Combien de pliages seront nécessaires pour créer une colonne en papier d’une hauteur permettant d’atteindre la Lune ?
