Pseudo-quadrature de Kochanski (1685)

La pseudo-quadrature de Kochansky permet de calculer la valeur de \pi avec 4 chiffres exacts après la virgule.

Construction :

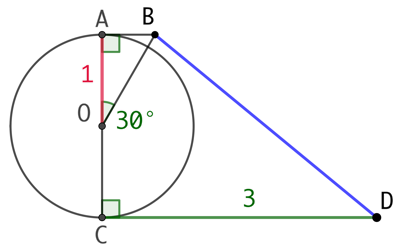
  • On trace un cercle de rayon 1. Soit [AC] l’un de ses diamètres.
  • On trace la perpendiculaire à (AC) passant par A.
  • On trace un angle de 30° de sommet O et de côté [OA]. L’autre côté de l’angle coupe la perpendiculaire au point B.
  • On trace la perpendiculaire à (AC) passant par B. Soit le point D tel que CD = 3 et situé dans le même demi-plan que B par rapport à (AC).
  • La distance BD est égale à 3,141533…

Explications :

Calcul de AB : \tan{\widehat{AOB}}=\tan \dfrac{\pi}{6}}=\dfrac{1}{\sqrt{3}}=\dfrac{AB}{1}=AB.

Calcul de BD : BD^2 = 2^2 + \left(3-\dfrac{1}{\sqrt{3}} \right)^2 = \dfrac{40}{3} - 2\sqrt{3}.
D’où BD = \sqrt{\dfrac{40}{3} - 2\sqrt{3}}, soit environ 3,1415.

Adam Adamandy Kochański (1631 – 1700) : mathématicien, physicien et horloger polonais

Print Friendly, PDF & Email