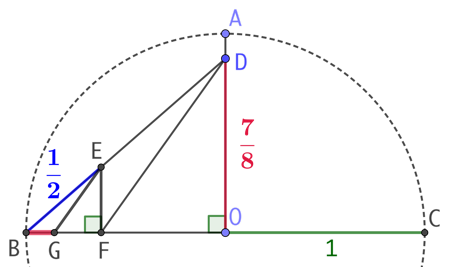
 La pseudo-quadrature de Jacob de Gelder permet de calculer la valeur de
La pseudo-quadrature de Jacob de Gelder permet de calculer la valeur de ![]() avec 6 chiffres après la virgule.
avec 6 chiffres après la virgule.
Explications :
On utilise le théorème de Thales dans le triangle BDF : ![]() .
.
Puis on utilise Thales dans le triangle BDO : ![]() .
.
De l’égalité ![]() , il vient
, il vient ![]() puisque
puisque ![]() .
.
À nouveau Thales dans le triangle BDO : ![]() , soit
, soit ![]() puisque
puisque ![]() , soit
, soit ![]() .
.
On utilise le théorème de Pythagore dans le triangle BFE : ![]() .
.
![]() . Soit
. Soit ![]() .
.
Ce qui donne pour BG environ 0,141592.
Jacob de Gelder (1765 – 1848) : mathématicien hollandais
