Proportionnalité

I – Grandeurs proportionnelles

Définition
Deux grandeurs sont proportionnelles lorsque les valeurs de l’une s’obtiennent en multipliant (ou en divisant) par un même nombre non nul les valeurs de l’autre.

Exemples :

Le périmètre d’un carré et la longueur de ses côtés sont proportionnels car on obtient le périmètre en multipliant la longueur du côté par 4. 4 est le coefficient de proportionnalité.

Dans l’aviation, on mesure l’altitude en “pied” et non en mètre. Un pied correspond à 0,3048 mètre. Pour convertir en mètres une longueur exprimée en pieds, on la multiplie par 0,3048. Dire qu’un avion vole à 10 000 pieds est équivalent à dire qu’il vole à 3 048 m car 10\:000 \times 0,3\:048 = 3\:048.

Les deux grandeurs, exprimées en pied et en mètre, sont donc proportionnelles. Le nombre 0,3 048 est appelé coefficient de proportionnalité.

ATTENTION : Deux grandeurs ne sont pas toujours proportionnelles. En voici quelques-unes qui ne le sont pas :

  • La taille d’une personne et son âge ;
  • l’aire d’un carré et la longueur de son côté.

II – Calculs dans une situation de proportionnalité

Pour illustrer une situation de proportionnalité, on utilise souvent un tableau appelé tableau de proportionnalité. Dans un tel tableau, on obtient les nombres de la seconde ligne en multipliant ceux de la première ligne par le coefficient de proportionnalité.

Exemple : Comment complèter le tableau de proportionnalité suivant ?

Première méthode : À l’aide du coefficient de proportionnalité

D’après le tableau de proportionnalité, on sait que 8 kg de pommes coûtent 7,68 €. On cherche le coefficient de proportionnalité, c’est-à-dire le nombre manquant dans la multiplication : 8 \times \cdots = 7,68. Ce nombre est égal à 7,68 \div 8 = 0,96. Cela signifie que un kilogramme de pommes coûte 0,96 €. Donc

  • deux kilogrammes coûtent 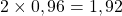2 \times 0,96 = 1,92 € et
  • 24 kilogrammes coûtent 24 \times 0,96 = 23,04 €.

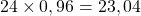On peut partiellement compléter le tableau de proportionnalité :

Pour remplir les deux cases de la première ligne, on peut remarquer que on peut acheter un kilogramme de pommes avec 0,96 €. Donc combien de kilogrammes peut-on acheter avec 9,60 € ? Il suffit de faire la division 9,6 \div 0,96 = 10. On peut donc acheter 10 kilogrammes de pommes avec 9,60 €.

Même méthode : Combien de kilogrammes peut-on acheter avec 15,36 € . On fait la division : 15,36 \div 0,96 = 16. On peut donc acheter 16 kilogrammes de pommes avec 15,36 €.

Le tableau de proportionnalité complet est :

Remarque : Dans un le tableau de proportionnalité, on obtient les nombres de la première ligne en divisant ceux de la seconde ligne par le coefficient de proportionnalité.

III – Propriétés de linéarité

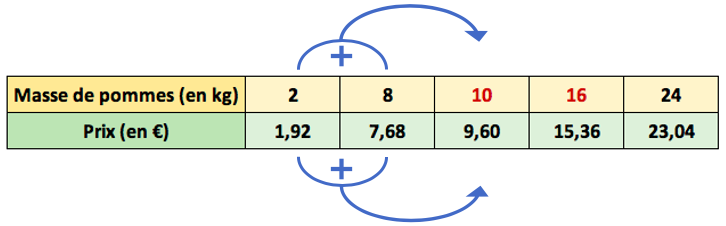
En reprenant l’exemple précédent, on remarque que la troisième colonnes de nombres s’obtient en additionnant les nombres des deux premières colonnes :

2 + 8 = 10 et 1,92 + 7,68 = 9,60

2 \times 5 = 10 et 1,92 \times 5 = 9,6

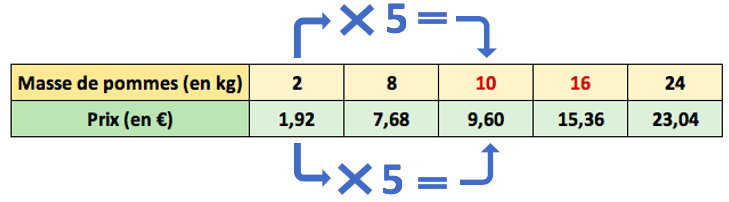
Ces propriétés de linéarité permettent souvent de compléter rapidement un tableau de proportionnalité.

IV – Partage selon un ratio

Exemple n°1 : La figure de droite se compose 27 carrés : 21 bleus et 6 rouges répartis en 9 colonnes de 3 carrés chacune.

En divisant le nombre de carrés de chaque couleur par le nombre de colonnes correspondant on obtient : \dfrac{21}{7} = \dfrac{6}{2} = 3.

En divisant le nombre total de carrés par le nombre total de colonnes, on obtient \dfrac{27}{9} = 3.

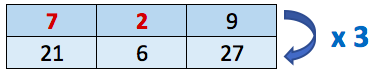On dit que les bleus et les rouges sont dans un ration 7 : 2.

Nous sommes dans une situation de proportionnalité. Voici son tableau de proportionnalité

Exemple n°2 : On veut répartir 60 € entre deux personnes dans un  ratio 3 : 2.

  1. On commence par remplir un tableau de proportionnalité avec les éléments fournis par l’énoncé.
  2. On calcule le coefficient  de proportionnalité quittait passer de 5 à 60. Pour cela on divise 60 par 5. On obtient 12.
  3. Connaissant le coefficient de proportionnalité, on complète le tableau. L’une des personne recevra 36 € et l’autre 24 €.

V – Échelle d’un plan

Définition
L’échelle d’un plan ou d’une carte est le coefficient de proportionnalité entre les mesures des distances reportées sur la carte ou le plan et les mesures des distances réelles.

Échelle = \dfrac{distances \: sur \: le \: plan}{distance \: réelle}

Ce rapport est constant et concerne l’ensemble des objets et des longueurs présents sur la carte ou le plan.

Souvent, l’échelle est exprimée sous la forme d’une fraction dont le numérateur est égal à 1.

Exemple :

L’échelle d’une carte, exprimée sous la forme \dfrac{1}{250\:000}, que l’on prononce “au 250 000 ème”, signifie qu’un 1 cm sur cette carte représente en réalité 250 000 cm sur le terrain, c’est-à-dire 2 500 m ou encore 2,5 km.

Nous pouvons utiliser l’égalité suivante : dimension \: réelle = dimension \: sur \: la \: carte \times {250\:000}.

Inversement, une distance 20 km sera représentée sur le plan par une longueur de 8 cm. Ce résultat est obtenu en utilisant l’égalité : dimension \: sur \: la \: carte = \dfrac{dimension \: réelle}{250\:000}

Print Friendly, PDF & Email