Prismes et cylindres

I – Prisme droit

Définition
un prisme droit est un solide qui possède deux faces polygonales parallèles et superposables qu’on appelle les bases, et plusieurs autres faces latérales toutes rectangulaires.

Définitions
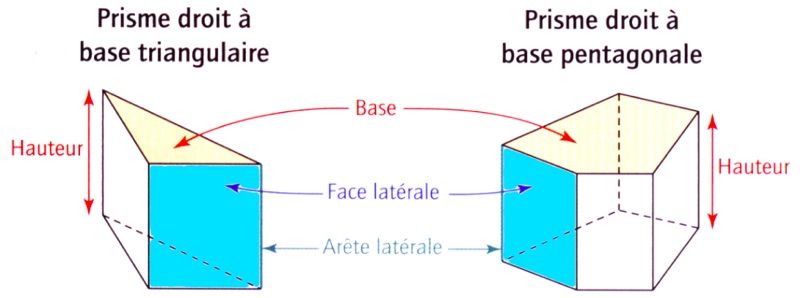
  • les côtés des bases et des faces latérales sont les arêtes du prisme droit.
  • les points d’intersection des arêtes sont les sommets du prisme droit.
Propriétés
  • Les arêtes latérales d’un prisme droit sont parallèles et possèdent la même longueur. Cette longueur est la hauteur du prisme droit.
  • La section d’un prisme droit par un plan parallèle à une de ses bases est un polygone parallèle et superposable à cette base.


Exemple du programme de sixième :

le parallélépipède rectangle (le pavé droit)

Patron d’un prisme

Définition
Un patron d’un solide est une surface plane qui, après pliage, permet de fabriquer ce solide.

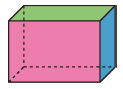Différents patrons du même pavé droit :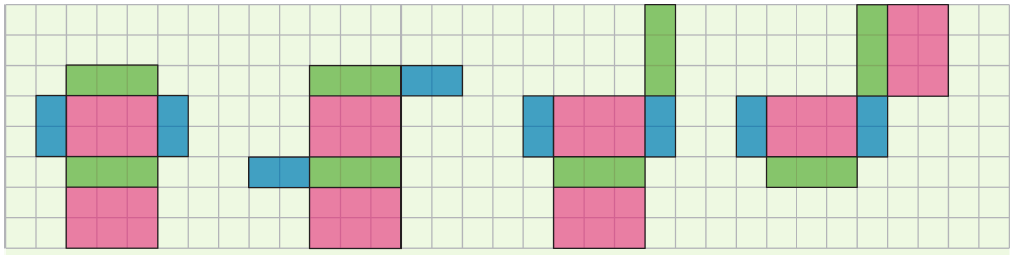

Patron d’un prisme à 4 faces latérales :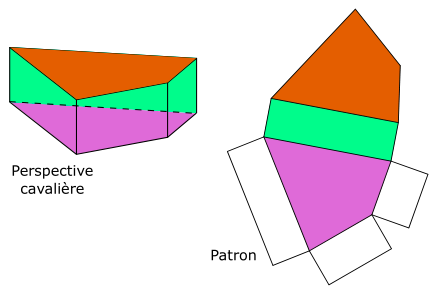

II – Représentation en perspective cavalière

Pour représenter un prisme droit (ou tout autre solide), on peut utiliser une perspective cavalière. Les trois règles de la perspective cavalière sont :

  1. Les arêtes d’une base sont parallèles à celle de l’autre base et de même dimension ;
  2. Les arêtes latérales sont toutes parallèles et de même longueur ;
  3. Les arêtes cachées sont représentées en pointillé.
Le plan du projet du château des Tuileries en 1578 réalisé en perspective cavalière
Le même plan en perspective linéaire.

III – Cylindre de révolution

Définition
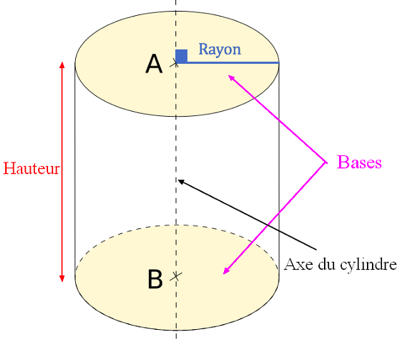Un cylindre de révolution est un solide qui possède deux faces parallèles et superposables qui sont des disques. La surface latérale est rectangle enroulé autour de ses bases.

L’axe du cylindre de révolution est la droite passant par les centres de ses bases et perpendiculaire à chaque base.

La hauteur d’un cylindre de révolution est la longueur du segment dont les extrémités sont les centres de ses bases

Pourquoi appelle-t-on cela un cylindre de révolution ?

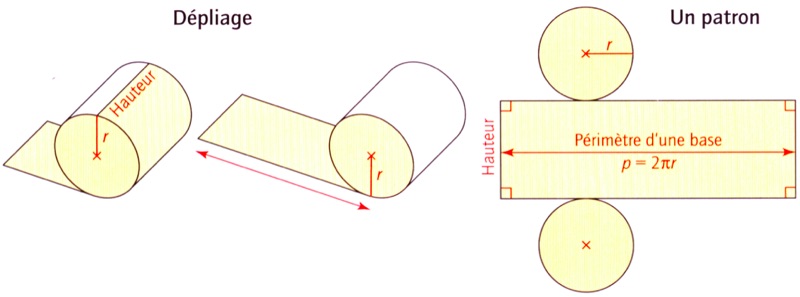
Patron d’un cylindre de révolution

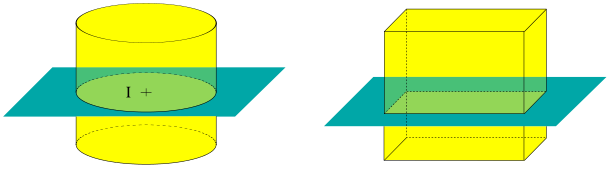
IV – Sections

Propriété
Lorsque l’on découpe un prisme droit ou un cylindre de révolution par un plan parallèle à l’une de ses bases, on obtient une section qui est parallèle et superposable à cette base.

V – Volumes

Calcul du volume d’un prisme droit :

  • La base du prisme a une aire : \mathcal{A}
  • La hauteur du prisme est : h
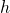
  • Alors le volume du prisme est donné par la formule : \mathcal{A} \times h

Calcul du volume d’un cylindre de révolution :

  • La rayon de la base du cylindre est : r
  • La hauteur du cylindre est : h
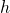
  • Alors le volume du cylindre est donné par la formule : 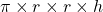\pi \times r \times r \times h que l’on note aussi 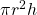\pi r^2 h. Une valeur approchée de 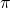\pi est 3,14.
Print Friendly, PDF & Email