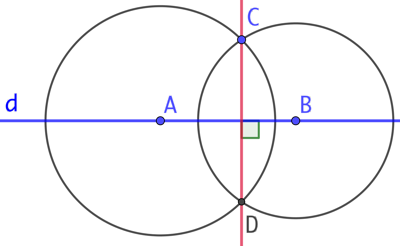
 Soit la droite d et un point C n’appartenant pas à cette droite. La droite perpendiculaire à d passant par C se construit ainsi :
Soit la droite d et un point C n’appartenant pas à cette droite. La droite perpendiculaire à d passant par C se construit ainsi :
- On place deux points A et B sur d et par trop éloignés de C.
- On construit les cercles de centres A et B passant par C.
- La droite (CD) est la perpendiculaire recherchée.
Explications :
Par construction les points C et D appartiennent au cercle de centre A. Donc A est équidistant de C et de D. Pour une raison similaire, B est équidistant de C et de D. Par conséquent les points A et B appartiennent à la médiatrice du segment [CD]. On peut donc affirmer que (AB) est la médiatrice de [CD] et que les droites (AB) et (CD) sont perpendiculaires.
Remarque : Cette construction est plus rapide que celle présentée dans l’article : Perpendiculaire d’une droite passant par un point (version 2).
