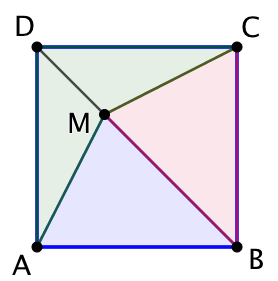
ABCD est un carré. Où placer le point M pour les aires de MAB, MBC et MCDA soient égales ?
Explications :
Oublions pour l’instant le quadrilatère MCDA. On va déterminer le lieu des points M tels que MAB et MBC ont la même aire.
Comme ABCD est un carré, ces deux triangles ont leurs bases, AB et BC, de même longueur. Pour qu’ils aient des aires égales, il faut que leurs hauteurs issues de M, MH et MK, soient de même longueur.
[BA) et [BC) sont les deux côtés de l’angle
. Le lieu des points équidistants des côtés d’un angle est sa bissectrice. ABCD est un carré donc cette bissectrice est la diagonale (BD).
Réintégrons MCDA dans la démonstration. Puisque M est sur la diagonale (BD), il est évident que celle-ci constitue un axe de symétrie pour MCDA. Par conséquent, on cherche la position de M pour laquelle le triangle DAM possède une aire égale à la moitié de celle de MAB.
Ces deux triangles partagent le même sommet A et leurs bases sont sur (AB). Il vient alors que 
.
Remarque : On obtient le même résultat si ABCD est un parallélogramme.
