I – Multiplication
- Les nombres que l’on multiplie s’appellent les facteurs.
- Le résultat d’une multiplication s’appelle le produit.
Exemple : On pose et on calcule : 
- Les nombres 83 et 117 sont les facteurs de la multiplication.
- Le résultat 9 711 est le produit.
Exemple : Comment calculer astucieusement 4 × 56 × 25 ?
4 × 56 × 25 = (4 × 25) × 56 = 100 × 56 = 5 600
Exemple : 7 x 3 + 6 x 5.
- On calcule les produits : 7 x 3 = 21 et 6 x 5 = 30
- Puis on fait la somme des produits : 21 + 30 = 51
II – Division euclidienne
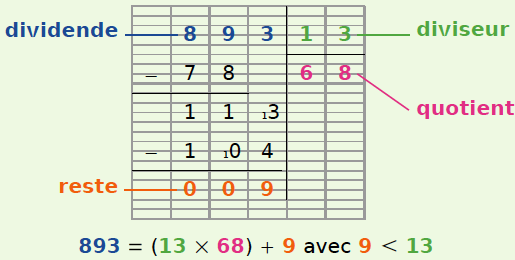
Exemple : On pose et on calcule la division de 893 par 13.
Exemple : Un fleuriste a reçu 260 roses. Il prépare des corbeilles de 12 roses chacune. Combien de corbeilles peut-il préparer ?
On cherche combien de fois il y a 12 dans 260 : 260 = (12 × 21) + 8 avec 8 < 12.
Il pourra donc préparer 21 corbeilles de 12 roses mais il lui restera 8 roses.
III – Divisibilité
1) Multiples et diviseurs d’un nombre entier
- Après avoir effectué la division euclidienne de 3 577 par 49, on obtient 3 577 = 49 × 73.
- Le reste étant nul, 3 577 est un multiple de 49 (et de 73 aussi !).
- On dit également que 3 577 est divisible par 49 ou que 49 est un diviseur de 3 577 ou que 49 divise 3 577.
2) Critères de divisibilité
- Un nombre entier est divisible par 2 si son chiffre des unités est 0, 2, 4, 6 ou 8.
- Un nombre entier est divisible par 3 si la somme de ses chiffres est un multiple de 3.
- Un nombre entier est divisible par 4 si le nombre formé par son chiffre des dizaines et son chiffre des unités (dans cet ordre) est un multiple de 4.
- Un nombre entier est divisible par 5 si son chiffre des unités est 0 ou 5.
- Un nombre entier est divisible par 9 si la somme de ses chiffres est un multiple de 9.
Exemple : On considère le nombre 23 928. Est-il divisible par 2, 5, 4, 3 et 9 ?
- Son chiffre des unités est 8 donc 23 928 est divisible par 2.
- Son chiffre des unités n’est ni 0 ni 5 donc 23 928 n’est pas divisible par 5.
- Le nombre formé par son chiffre des dizaines et son chiffre des unités est 28 qui est divisible par 4 donc 23 928 est divisible par 4.
- La somme de ses chiffres : 2 + 3 + 9 + 2 + 8 soit 24 est un multiple de 3 donc 23 928 est divisible par 3.
- La somme de ses chiffres : 2 + 3 + 9 + 2 + 8 soit 24 n’est pas un multiple de 9 donc 23 928 n’est pas divisible par 9.
IV – Opérations sur les durées
1) Conversion de durées
- Il y a 24 heures dans une journée
- Il y a 60 minutes dans une heure
- Il y a 60 secondes dans une minute.
Exemple : Combien y a-t-il de minutes dans 5 h 27 min ?
Exemple : Combien y a-t-il de secondes dans 2 h 47 min 53 s ?
Exemple : Combien y a-t-il d’heures, minutes et secondes dans 41 000 s ?
2) Addition de durées
Exemple : Un match dure 3 h 38 min et le suivant dure 2 h 49 min. Quelle est la durée totale de ces deux matchs ?
On effectue deux additions indépendantes : les minutes entre elles et les heures entre elles.
Mais le nombre de minutes obtenu est 87 qui est supérieur à 59. On va donc le convertir en heures et minutes sachant que 60 min = 1 h. 5 h 87 = 5 h + 60 + 27 = 6 h 27 min
La durée totale de ces deux matchs est donc de 6 h 27 min.
3) Soustraction de durées
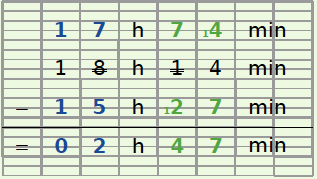Exemple : Un film débute à 15 h 27 et finit à 18 h 14. Quelle est la durée de ce film ?
On effectue deux soustractions indépendantes : les minutes entre elles et les heures entre elles.
Mais on ne peut pas enlever 27 à 14. On va donc convertir 1 des 18 heures en 60 min. 18 h 14 min = 17 h + 1 h 14 min = 17 h + 60 min + 14 min = 17 h 74 min.
Ce film dure donc 2 h 47 min.
EXERCICES
- 2 / 18 : division euclidienne
- 4 / 18 : divisibilité
- 5 / 18 : durée
- 9 / 19 : calcul astucieux
- 12 / 19 : multiplication posée
- 16 / 19 : texte à traduire en expression
- 17 / 19 : expression à traduire en texte
- 18 / 19 : trouver un produit sans calculer à partir d’un exemple donné
- 19 / 19 : priorité x versus +
- 20 / 19 : idem
- 22 / 20 : vocabulaire de la division euclidienne
- 27 / 20 : division euclidienne
- 28 / 20 : division euclidienne
- 34 / 20 : division euclidienne
- 40 / 21: multiple
- 43 / 22 : multiple
- 49 / 22 : multiple
- 58 / 23 : durée
- 61 / 23 : conversion de durée
- 64 / 23 : durée
- 67 / 23 : durée
Problèmes
- 69 / 24 : Longueurs, aires
- 70 / 24 : abonnement
- 74 / 24 : programme de calcul
- 76 / 24 : nombre inconnu
- 80 / 25 : PGCD
