I – Milieu d’un segment
- Le milieu du segment [AB] est le point du segment [AB] qui est équidistant (à la même distance) des extrémités A et B.
- Dit autrement : Le milieu d’un segment coupe ce segment en deux segments de même longueur.
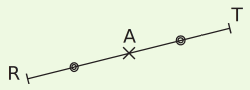 Exemple : Le point A est le milieu du segment [RT]. Cela signifie que les points A,R et T sont alignés et que les distances AR et AT sont égales.
Exemple : Le point A est le milieu du segment [RT]. Cela signifie que les points A,R et T sont alignés et que les distances AR et AT sont égales.
Codage du milieu : Pour indiquer sur une figure que deux segments ont la même longueur, on leur ajoute un même symbole (un petit disque noir dans cet exemple).
II – Vocabulaire du cercle
- Un cercle de centre O est l’ensemble des points situés à la même distance du point O.
- Cette distance est le rayon du cercle.
- Un diamètre d’un cercle est un segment ayant pour extrémités deux points de ce cercle et contenant son centre.
- Une corde d’un cercle est un segment ayant pour extrémités deux points de ce cercle.
- Un arc de cercle est une portion de cercle comprise entre deux points de ce cercle.
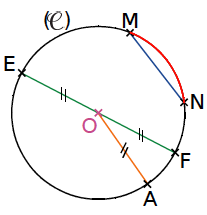 Exemple :
Exemple :
- Le point O est le centre du cercle
 .
. - Le segment [OA] est un rayon du cercle
- Le segment [EF] est un diamètre du cercle
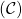
- Le segment [MN] est une corde du cercle
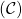
- La portion de cercle
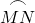 comprise entre M et N est un arc du cercle
comprise entre M et N est un arc du cercle 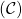
- Un cercle possède une infinité de rayons. Dans l’exemple précédent, les segments [OA], [OE] et [OF] sont trois rayons du cercle
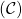 . LE rayon d’un cercle est la longueur de tous ses rayons : les trois distances OA, OE et OF sont toutes égales au rayon du cercle.
. LE rayon d’un cercle est la longueur de tous ses rayons : les trois distances OA, OE et OF sont toutes égales au rayon du cercle. - De la même façon, un cercle a une infinité de diamètres. LE diamètre d’un cercle est la longueur de tous ses diamètres.
Exemple : Si le rayon d’un cercle est de 3 cm alors son diamètre est de 6 cm.
III – Médiatrice d’un segment
 Exemple : La droite (d) est la médiatrice du segment [AB]. Elle passe par le point M, milieu du segment [AB]. Elle forme avec [AB] un angle droit.
Exemple : La droite (d) est la médiatrice du segment [AB]. Elle passe par le point M, milieu du segment [AB]. Elle forme avec [AB] un angle droit.
Construction de la médiatrice d’un segment
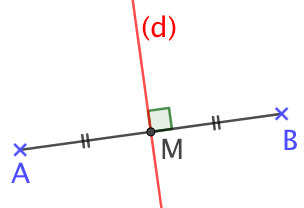
 On va utiliser les propriétés précédentes pour construire la médiatrice d’un segment [AB ]à l’aide d’une règle non graduée et d’un compas. Voici les étapes de construction :
On va utiliser les propriétés précédentes pour construire la médiatrice d’un segment [AB ]à l’aide d’une règle non graduée et d’un compas. Voici les étapes de construction :
- On trace le cercle de centre A qui passe par B.
- On trace le cercle de centre B qui passe par A.
- Ces deux cercles se croisent aux points C et D.
- La droite (CD) est la médiatrice du segment [AB].
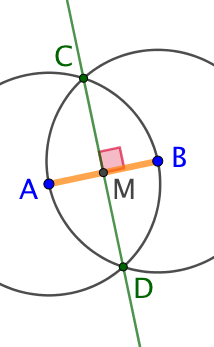
Pourquoi la droite (CD) est la médiatrice de [AB] ?
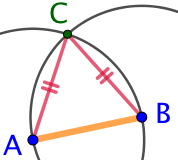 Les deux cercles que nous avons tracés ont le même rayon dont la longueur est AB.
Les deux cercles que nous avons tracés ont le même rayon dont la longueur est AB.
Le point C appartient au cercle de centre A, donc la distance AC est égale à la distance AB. Mais le point C appartient aussi au cercle de centre B, donc la distance BC est aussi égale à la distance AB. Par conséquent, les deux distances AC et AB sont égales. On en conclut que le point C appartient à la médiatrice du segment [AB].
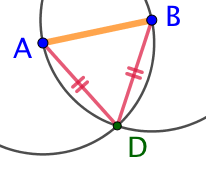 Nous pouvons faire exactement la même observation avec le point D et conclure que le point D appartient à la médiatrice du segment [AB].
Nous pouvons faire exactement la même observation avec le point D et conclure que le point D appartient à la médiatrice du segment [AB].
