Lieux géométrique des points dont la somme des distances à deux droites est constant

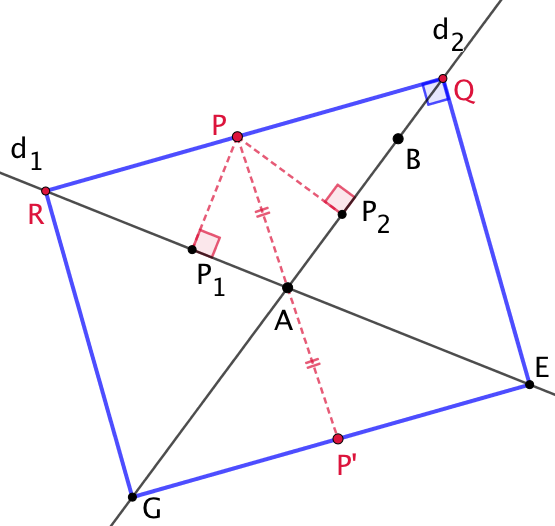
Soient deux droites et sécantes en A. Le lieu des points dont la somme des distances à et à est constante est constitué des quatre côtés d’un rectangle.

Construction :

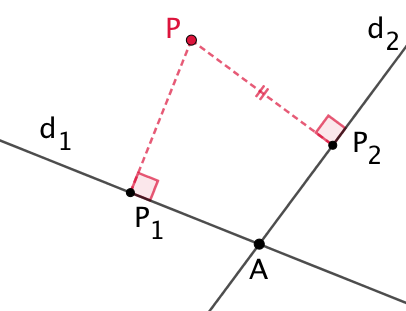
Soit P un point de ce lieu. Notons .

Soit le point de la droite tel que . Alors .

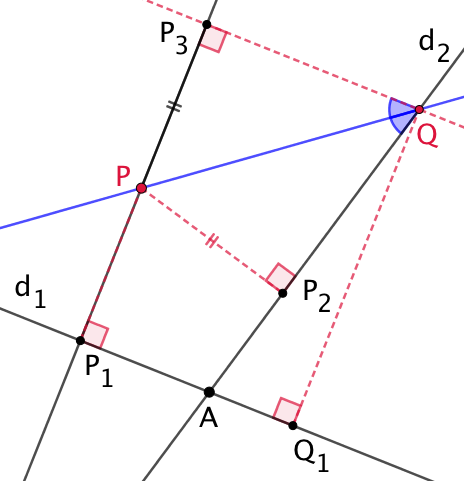
On trace la droite perpendiculaire à passant par . Cette droite coupe en Q.

est le projeté orthogonal de Q sur . donc Q appartient au lieu géométrique. Q est un point limite du lieu géométrique car une des deux distances, celle à est nulle.

Puisque P est à égale distance de et de , alors il appartient à la bissectrice de l’angle .

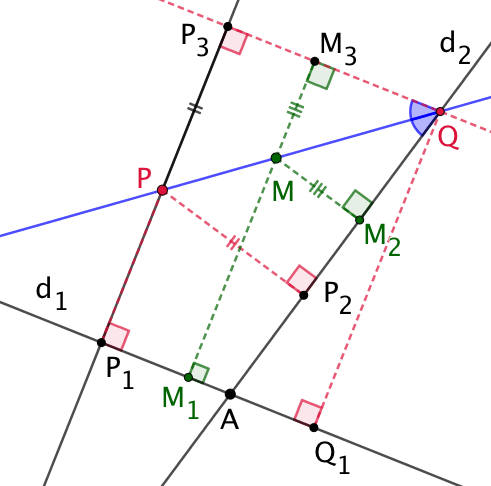Soient M un point de la droite , et les projetés orthogonaux respectifs de M sur et . M appartient à la bissectrice de donc .

Or donc . Par conséquent le point M appartient au lieu recherché.

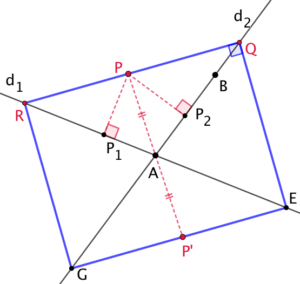Le point R, intersection de la droite et de est un autre point limite du lieu géométrique car une des deux distances, celle à est nulle. Ainsi le segment [RQ] est inclus dans le lieu géométrique.

Par symétrie par rapport à A, le segment [EG] est aussi inclus dans le lieu géométrique. On complète ce lieu avec les segments [QE] et [GR].

Voir aussi : Lieux géométrique des points dont la différence des distances à deux droites est constant