I – Comment représenter un déplacement rectiligne ?
| Soient deux points |
Soit un point |
|
 |
 |
 |
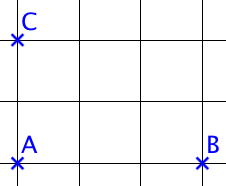
Si on voulait définir de manière parfaitement claire (univoque) ce déplacement à une personne ne voyant pas ces figures, il faudrait lui donner les trois informations suivantes :
- le déplacement est horizontal ;
- le déplacement d’effectue de la gauche vers la droite ;
- le déplacement est de 3 unités de longueurs
Les mathématiciens ont donné un nom à ce type de déplacement : une translation.
Une translation est parfaitement définie par le vecteur qui lui est associé et qui possède trois caractéristiques :
- sa direction : horizontale, verticale, diagonale
- son sens : gauche vers droite, haut vers bas, sud vers nord, …
- sa norme, sa « longueur« .
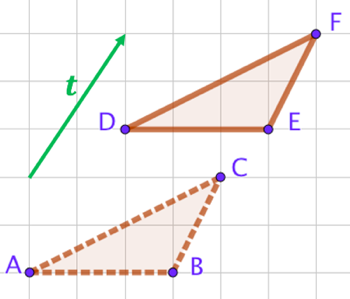 Exemple : Sur la figure de droite, nous avons représenté un triangle
Exemple : Sur la figure de droite, nous avons représenté un triangle ![]() et une translation définie par son vecteur
et une translation définie par son vecteur ![]() .
.
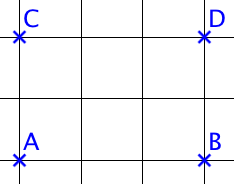
En langage simple, on peut dire que la translation de vecteur ![]() déplace un point
déplace un point
- de deux carreaux vers la gauche puis de trois carreaux vers le haut,
- ou de trois carreaux vers le haut, puis de deux carreaux vers la droite.
Les 3 caractéristiques du vecteur ![]() sont :
sont :
- direction : en diagonale selon la segment vert
- sens : du coin gauche en bas vers le point droite en haut
- norme : l’hypoténuse d’un triangle de côtés 2 et 3, ce qui donne
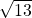 d’après le théorème de Pythagore.
d’après le théorème de Pythagore.
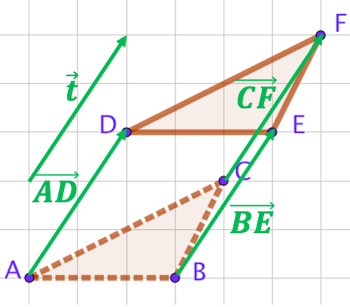 Cette translation de vecteur
Cette translation de vecteur ![]() déplace le point
déplace le point ![]() vers le point
vers le point ![]() ,
, ![]() vers
vers ![]() et
et ![]() vers
vers ![]() . Ainsi l’image du triangle
. Ainsi l’image du triangle ![]() par cette translation est le triangle
par cette translation est le triangle ![]() .
.
Remarque :
On aurait pu tout aussi bien définir cette translation en la décrivant comme le déplacement du point ![]() vers le point
vers le point ![]() par exemple. Le vecteur
par exemple. Le vecteur ![]() a exactement les mêmes caractéristiques que le vecteur
a exactement les mêmes caractéristiques que le vecteur ![]() : même direction, même sens et même norme.
: même direction, même sens et même norme.
Finalement, il apparaît que les vecteurs ![]() ,
, ![]() ,
, ![]() et
et ![]() représentent la même translation. On dira qu’ils sont égaux.
représentent la même translation. On dira qu’ils sont égaux.
II – Définitions et vocabulaire
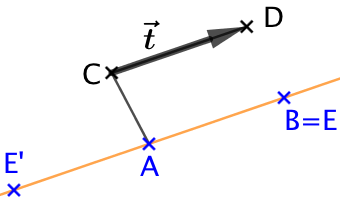
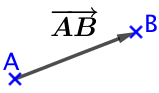 Le point
Le point  est l’origine du vecteur.
est l’origine du vecteur.- Le point
 est l’extrémité du vecteur.
est l’extrémité du vecteur. - On représente le vecteur
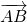 par une flèche allant de
par une flèche allant de  jusqu’à
jusqu’à  .
.
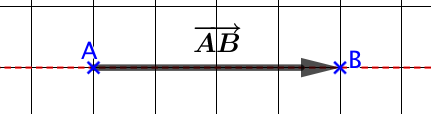 sa direction : la droite (AB)
sa direction : la droite (AB)- son sens : de
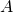 vers
vers 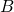
- sa norme : la longueur
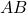 que l’on note
que l’on note 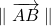
Dans l’exemple de droite, ![]()
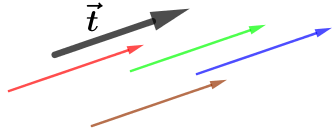 Deux vecteurs sont égaux si et seulement si ces deux vecteurs possèdent la même direction, le même sens, la même norme.
Deux vecteurs sont égaux si et seulement si ces deux vecteurs possèdent la même direction, le même sens, la même norme.
Dans la figure de droite, tous les vecteurs sont égaux à ![]() .
.
Précision importante : Dire que deux vecteurs possèdent la même direction signifie qu’is sont portés par deux droites parallèles. Il n’est donc pas nécessaire que ce soit la même droite.
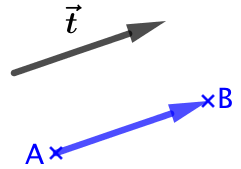 Soit un vecteur
Soit un vecteur Démonstration : Soient ![]() et
et ![]() l’origine et l’extrémité du vecteur
l’origine et l’extrémité du vecteur ![]() .
.
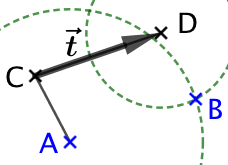 1ère partie (existence) : On construit le point
1ère partie (existence) : On construit le point ![]() de telle façon que le quadrilatère
de telle façon que le quadrilatère ![]() (attention à l’ordre des lettres) soit un parallélogramme :
(attention à l’ordre des lettres) soit un parallélogramme :
- On trace un arc de cercle de centre A et de rayon
 ;
; - On trace un arc de cercle de centre D et de rayon
 ;
; - L’une des deux intersections des arcs de cercle est le point
 .
.
Puisque ![]() est un parallélogramme, ces côtés opposés sont parallèles et de même longueur. En particulier les droites
est un parallélogramme, ces côtés opposés sont parallèles et de même longueur. En particulier les droites ![]() et
et ![]() sont parallèles et les distances
sont parallèles et les distances ![]() et
et ![]() sont égales. Par conséquent les vecteurs
sont égales. Par conséquent les vecteurs ![]() et
et ![]() sont égaux, car dans le même sens. On a donc trouvé un point B tel que
sont égaux, car dans le même sens. On a donc trouvé un point B tel que ![]() .
.
 2ème partie (unicité) : Supposons qu’il existe un autre point
2ème partie (unicité) : Supposons qu’il existe un autre point ![]() tel que
tel que ![]() . Alors
. Alors ![]() .
.
Donc les droites (AB) et (AE) seraient parallèles. Mais deux droites parallèles ayant un point en commun sont confondues. Par conséquent le point ![]() serait sur la droite (AB).
serait sur la droite (AB).
Si ![]() , alors les distances
, alors les distances ![]() et
et ![]() seraient égales. Comme le montre la figure ci-dessus, cela laisse deux possibilités pour la position du point
seraient égales. Comme le montre la figure ci-dessus, cela laisse deux possibilités pour la position du point ![]() sur la droite
sur la droite ![]() : Soit
: Soit ![]() et
et ![]() sont confondus, soit
sont confondus, soit ![]() est le symétrique de
est le symétrique de ![]() par rapport à
par rapport à ![]() (position
(position ![]() ).
).
Or la position ![]() est à rejeter car les vecteurs
est à rejeter car les vecteurs ![]() n’ont pas le même sens. Conclusion
n’ont pas le même sens. Conclusion ![]() , ce qui achève de démontrer que le point
, ce qui achève de démontrer que le point ![]() est unique.
est unique.
Remarque : On dit que ![]() est un représentant du vecteur
est un représentant du vecteur ![]() .
.
 Démonstration :
Démonstration :
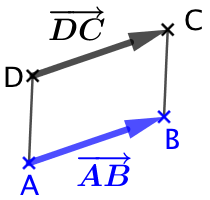
1ère partie : Supposons que ABCD soit un parallélogramme. Alors :
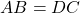 , donc
, donc 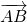 et
et 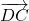 ont la même norme.
ont la même norme.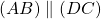 , donc
, donc 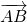 et
et 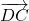 ont la même direction.
ont la même direction.
Ces deux vecteurs ont évidemment le même sens. Conclusion, ils sont égaux.
2ème partie (réciproque) : Supposons que ![]() . Alors
. Alors ![]() et
et ![]() . Donc
. Donc ![]() est un quadrilatère dont deux côtés sont parallèles et de même dimension. Comme ces deux vecteurs ont le même sens, ce quadrilatère n’est pas croisé. On en conclut que c’est un parallélogramme.
est un quadrilatère dont deux côtés sont parallèles et de même dimension. Comme ces deux vecteurs ont le même sens, ce quadrilatère n’est pas croisé. On en conclut que c’est un parallélogramme.
Autrement dit, pour tout point ![]() ,
, ![]() .
.
Remarque : le vecteur nul n’a pas de sens et pas de direction. Sa norme vaut 0.
III – Somme de deux vecteurs
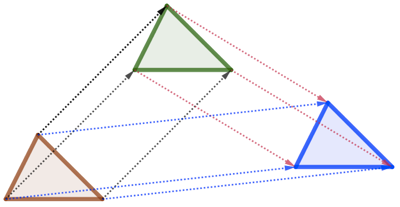
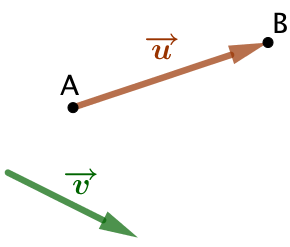
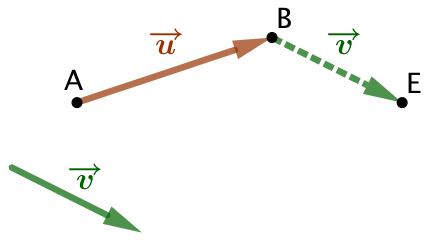
Pour transformer le triangle marron en triangle bleu, on peut opérer de deux façons différentes :
- Soit par une translation directe du marron vers le bleu ;
- Soit par deux translations : du marron vers le vert, puis du vert vers le bleu.
Soient alors :
 le vecteur associé à la transformation du marron vers le vert ;
le vecteur associé à la transformation du marron vers le vert ; le vecteur associé à la transformation du vert vers le bleu ;
le vecteur associé à la transformation du vert vers le bleu ; le vecteur associé à la transformation du marron vers le bleu.
le vecteur associé à la transformation du marron vers le bleu.
Alors on dira que ![]() .
.
Construction de la somme de deux vecteurs
| Soient On suppose que l’origine et l’extrémité du vecteur |
 |
| On construit un vecteur égal au vecteur |
 |
| Alors la somme Donc l’origine du vecteur somme est l’origine du premier vecteur et l’extrémité du vecteur somme est l’extrémité du second vecteur. |
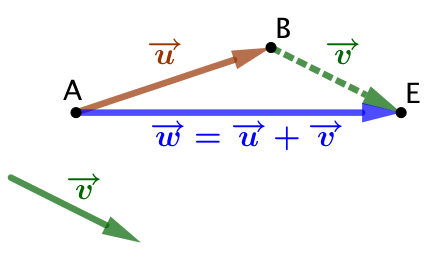 |
Bien entendu, on peut aussi partir du vecteur ![]() :
:
| On suppose que l’origine et l’extrémité du vecteur |
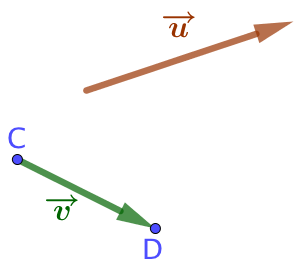 |
| On construit un vecteur égal au vecteur |
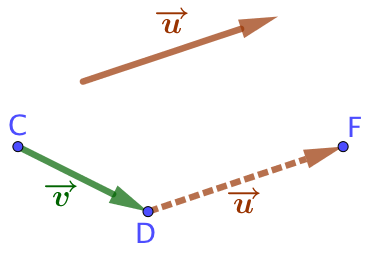 |
| Alors la somme Bien évidemment |
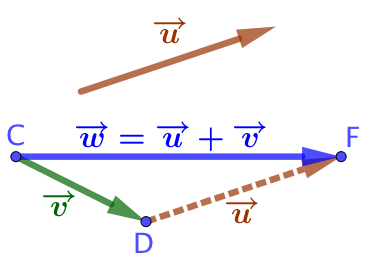 |
Ainsi on aura démontrer que les deux constructions du vecteur somme, que nous venons de découvrir, donnent le même résultat
Démonstration : 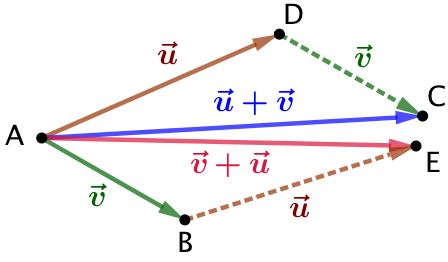 Soient deux vecteurs
Soient deux vecteurs ![]() et
et ![]() représentés par
représentés par ![]() et
et ![]() . On construit le vecteur
. On construit le vecteur ![]() représenté par
représenté par ![]() et le vecteur
et le vecteur ![]() représenté par
représenté par ![]() .
.
On va démontrer que les points C et E sont confondus. (La figure de droite est volontairement fausse).
Par construction ![]() donc, d’après une propriété démontrée précédemment, ABED est un parallélogramme.
donc, d’après une propriété démontrée précédemment, ABED est un parallélogramme.
Par construction ![]() donc ABCD est aussi un parallélogramme.
donc ABCD est aussi un parallélogramme.
On sait que si trois points R, S et T sont donnés, il existe un quatrième point unique U tel RSTU soit un parallélogramme. Or nous venons de voir que ABCD et ABED sont deux parallélogrammes, alors nécessairement C et E sont confondus. Ce qui achève de démontrer que ![]() .
.
![]() ,
, ![]() et
et ![]() ,
, ![]() .
.
C’est une conséquence directe de la définition de la somme de deux vecteurs.
La relation de Chasles est une propriété importante.
Remarque : une conséquence de cette relation a déjà été étudiée au collège : l’inégalité triangulaire.
Démonstration :
Si les deux vecteurs ![]() et
et ![]() sont égaux alors ils ont la même direction. Donc les droites
sont égaux alors ils ont la même direction. Donc les droites ![]() et
et ![]() sont parallèles. Or deux droites parallèles possédant un point en commun sont confondues. Donc les points
sont parallèles. Or deux droites parallèles possédant un point en commun sont confondues. Donc les points ![]() ,
, ![]() et
et ![]() sont alignés.
sont alignés.
Si les deux vecteurs ![]() et
et ![]() sont égaux alors ils ont le même sens. Donc sur la droite
sont égaux alors ils ont le même sens. Donc sur la droite ![]() , les points
, les points ![]() et
et ![]() sont du même côté par rapport à
sont du même côté par rapport à ![]() .
.
Si les deux vecteurs ![]() et
et ![]() sont égaux alors ils ont la même norme. Donc
sont égaux alors ils ont la même norme. Donc ![]() .
.
Conclusion : les points ![]() et
et ![]() sont nécessairement confondus.
sont nécessairement confondus.
 Démonstration :
Démonstration :
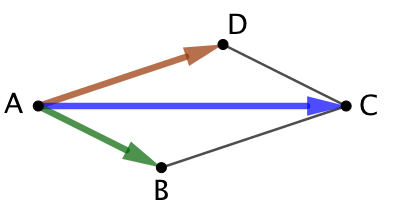
1ère partie : Supposons que ABCD soit un parallélogramme. Alors ![]() .
.
En utilisant la relation de Chasles, il vient : ![]() .
.
2ème partie (réciproque) : Supposons que ![]() .
.
Soit ![]() le point tel que
le point tel que ![]() soit un parallélogramme. Alors
soit un parallélogramme. Alors ![]() .
.
En utilisant la relation de Chasles, il vient : ![]() .
.
Donc ![]() , ce qui prouve que
, ce qui prouve que ![]() . Donc
. Donc ![]() est un parallélogramme.
est un parallélogramme.
IV – Vecteur opposé
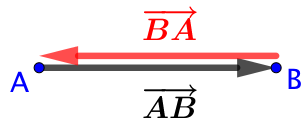
Soit ![]() , l’opposé de
, l’opposé de ![]() vérifie la relation :
vérifie la relation : ![]() . On va adopter la même approche avec les vecteurs.
. On va adopter la même approche avec les vecteurs.
 Soient point
Soient point ![]() et
et ![]() .
.
On sait que ![]() . Appliquons la relation de Chasles au vecteur
. Appliquons la relation de Chasles au vecteur ![]() :
: ![]() .
.
Donc ![]() .
.
De manière générale, soit un vecteur ![]() . L’opposé de
. L’opposé de ![]() , noté
, noté ![]() vérifie la relation :
vérifie la relation : ![]() .
.
Construction de la différence de deux vecteurs
On note : ![]() .
.
| Soient deux vecteurs |
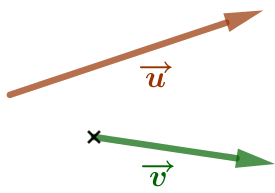 |
| On trace le vecteur |
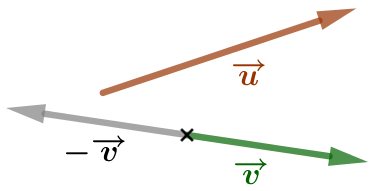 |
| On trace un représentant du vecteur |
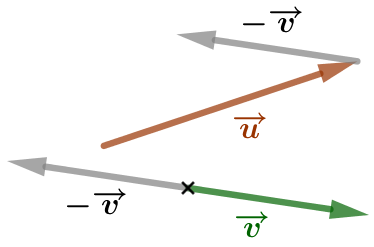 |
| On construit la somme des vecteurs |
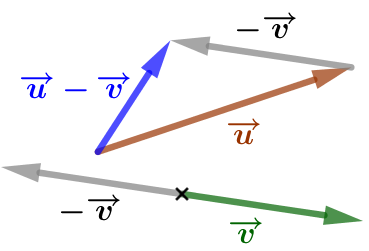 |
Démonstration : Supposons que ![]() . On peut ajouter le même vecteur aux deux membres de l’égalité :
. On peut ajouter le même vecteur aux deux membres de l’égalité :
![]() . Comme
. Comme ![]() , il vient :
, il vient : ![]()
Remarque : Cette propriété ressemble à une propriété similaire des nombres : Si ![]() alors
alors ![]() .
.
EXERCICES
- 27 / 184 : Repérer des vecteurs égaux ou opposés, translations
- 29 / 184 : Repérer des vecteurs égaux sur une figure
- 31 / 185 : Construction de points
- 33 / 185 : Construction de points et vecteurs
- 35 / 185 : Raisonnement avec des vecteurs
- 38 / 186 : Raisonnement avec des vecteurs
- 40 / 186 : Relation de Chasles
- 42 / 187 : Somme de vecteurs
- 75 / 193 : Raisonnement avec des vecteurs
- 73 / 192 : Raisonnement avec des vecteurs + Geogebra
