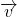I – Milieu
- Le point
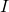 est le milieu du segment
est le milieu du segment ![Rendered by QuickLaTeX.com [AB]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-9fd566b0e28516ed5c7d24192dac3fe1_l3.png) ;
; 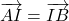 ;
;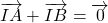 ;
;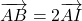 ;
;
Démonstration :
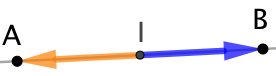
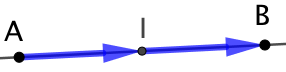 1ère partie : Supposons que le point
1ère partie : Supposons que le point ![]() soit le milieu du segment
soit le milieu du segment ![]() . Alors nous en déduisons que :
. Alors nous en déduisons que :
- les points
 ,
,  et
et 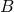 sont alignés, donc les vecteurs
sont alignés, donc les vecteurs 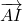 et
et 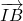 ont la même direction.
ont la même direction. 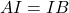 (égalité de distance), donc les vecteurs
(égalité de distance), donc les vecteurs 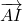 et
et 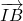 ont la même norme.
ont la même norme.
Et ils ont évidemment le même sens. Donc ![]() .
.
 2ème partie : Supposons que
2ème partie : Supposons que ![]() .
.
Alors ![]() .
.
Donc ![]() . Ce qui donne :
. Ce qui donne : ![]()
 3ème partie : Supposons
3ème partie : Supposons ![]() .
.
Alors la relation de Thales appliquée à ![]() donne :
donne : ![]() .
.
Donc ![]() , soit
, soit ![]() .
.
On obtient après simplification : ![]() .
.
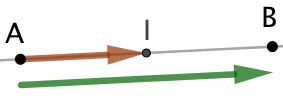
4ème partie : Supposons ![]() . On en déduit que :
. On en déduit que :
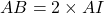 (égalité de longueur)
(égalité de longueur)- les vecteurs
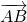 et
et 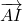 sont colinéaires, donc les points
sont colinéaires, donc les points 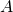 ,
, 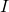 et
et 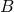 sont alignés.
sont alignés.
Cela permet d’affirmer que le point I est le milieu du segment ![]() .
.
II – Coordonnées d’un vecteur
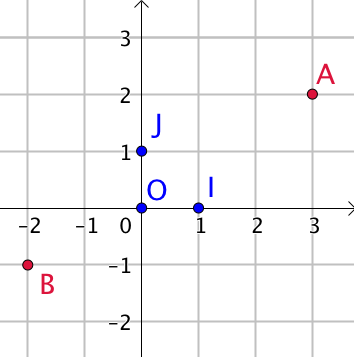 Un repère orthonormé est constitué de trois points
Un repère orthonormé est constitué de trois points - La droite
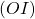 est l’axe des abscisses, c’est l’axe horizontal.
est l’axe des abscisses, c’est l’axe horizontal. - La droite
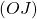 est l’axe des ordonnées, c’est l’axe vertical.
est l’axe des ordonnées, c’est l’axe vertical.
Le repère est noté : ![]()
Tout point du plan est repéré de manière unique grâce à ses deux coordonnées appelées abscisse et ordonnée.
Exemples:
- Les coordonnées du point
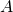 sont
sont 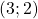
- Les coordonnées du point
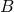 sont
sont 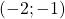
 Exemple :
Exemple :
Soient les point ![]() ainsi que les points
ainsi que les points ![]() le projeté de M sur l’axe des abscisses et
le projeté de M sur l’axe des abscisses et ![]() le projeté de M sur l’axe des ordonnées.
le projeté de M sur l’axe des ordonnées.
On a l’égalité : ![]()
![]()
![]()
Donc ![]()
On dit que les coordonnées du vecteur ![]() dans la base
dans la base ![]() sont
sont ![]() et
et ![]() .
.
On observe que les coordonnées du point ![]() et du vecteur
et du vecteur ![]() sont identiques.
sont identiques.
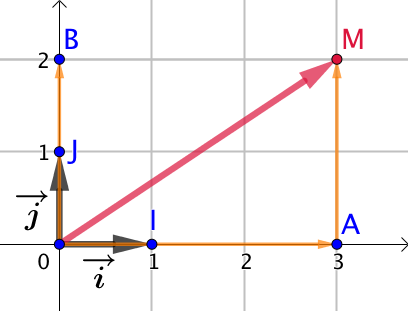
Remarque : Que ce passe-t-il si le vecteur n’a pas le point O comme origine ?
 Exemple :
Exemple :
Soit le vecteur ![]() égal au vecteur
égal au vecteur ![]() . Alors on doit s’attendre à ce que les coordonnées de
. Alors on doit s’attendre à ce que les coordonnées de ![]() soient
soient ![]() . Ce que l’on va vérifier.
. Ce que l’on va vérifier.
![]()
![]() et
et ![]() .
.
Par conséquent ![]() . On retrouve les coordonnées de
. On retrouve les coordonnées de ![]() .
.
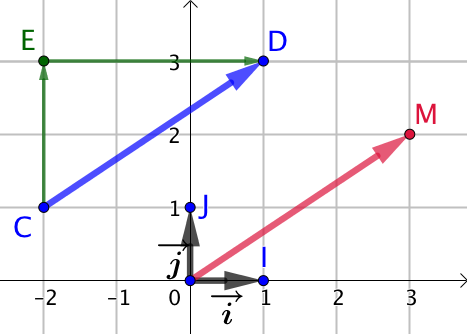
Pour tout vecteur ![]() , il existe un couple unique de réels
, il existe un couple unique de réels ![]() tels que
tels que ![]()
![]() et
et ![]() sont les coordonnées du vecteur
sont les coordonnées du vecteur ![]() dans la base orthonormée
dans la base orthonormée ![]()
Cas particulier : les coordonnées de ![]() sont
sont ![]() .
.
 Démonstration :
Démonstration :
Soit le repère orthonormé ![]() tel que
tel que ![]() et
et ![]() .
.
Existence de ![]() et de
et de ![]() :
:
Soit un vecteur ![]() et soit un point
et soit un point ![]() tel que
tel que ![]() .
.
Soit ![]() et
et ![]() les coordonnées du point
les coordonnées du point ![]() dans la repère
dans la repère ![]() . Alors on sait montrer que
. Alors on sait montrer que ![]() .
.
Donc ![]() .
.
Unicité de ![]() et de
et de ![]() : Supposons que
: Supposons que ![]()
Soient les points ![]() et
et ![]() tels que
tels que ![]() et
et ![]()
Alors ![]() donc
donc ![]() . Si ces deux points sont confondus, leurs coordonnées sont égales, donc
. Si ces deux points sont confondus, leurs coordonnées sont égales, donc ![]() et
et ![]() .
.
Pour tous vecteurs ![]() et
et ![]() , et pour tout nombre réel
, et pour tout nombre réel ![]() :
:
- les coordonnées du vecteur
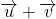 sont
sont 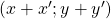 .
. - les coordonnées du vecteur
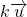 sont
sont 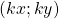 .
.
Cas particulier : si les coordonnées de ![]() sont
sont ![]() alors les coordonnées de son opposé,
alors les coordonnées de son opposé, ![]() sont
sont ![]()
Démonstration :
On sait que ![]() et que
et que ![]()
![Rendered by QuickLaTeX.com \[ $\overrightarrow{u} + \overrightarrow{v} = x \overrightarrow{i} + y \overrightarrow{j} + x' \overrightarrow{i} + y' \overrightarrow{j} = x \overrightarrow{i} + x' \overrightarrow{i} + y \overrightarrow{j} + y' \overrightarrow{j} = (x + x') \overrightarrow{i} + (y + y')\overrightarrow{j} \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-3c8f9517fcff0239cc3dfd2fb67a6095_l3.png)
Ce qui démontre que les coordonnées du vecteur ![]() sont
sont ![]()
![]() .
.
Ce qui démontrer que les coordonnées du vecteur ![]() sont
sont ![]() .
.
Si on remplace ![]() par
par ![]() , on démontre que les coordonnées de
, on démontre que les coordonnées de ![]() sont
sont ![]()
Dans la suite de ce chapitre, les points sont repérés par un repère orthonormé ![]() et les vecteurs par une base orthonormée
et les vecteurs par une base orthonormée ![]() , telle que
, telle que ![]() et
et ![]()
Autrement dit les coordonnées du milieu d’un segment sont les demi-sommes des extrémités de segment.
Démonstration :
Soit ![]() le milieu de [AB]. Nous savons que
le milieu de [AB]. Nous savons que ![]() .
.
La relation de Chasles appliquée à ![]() donne :
donne : ![]() .
.
Après développement, il vient : ![]() , soit
, soit ![]()
La relation de Chasles appliquée à ![]() donne :
donne : ![]() .
.
Sachant que ![]() , on obtient :
, on obtient : ![]() .
.
Les coordonnées de ![]() et de
et de ![]() sont respectivement
sont respectivement ![]() et
et ![]() , donc celles de
, donc celles de ![]() sont
sont ![]() qui sont aussi les coordonnées de
qui sont aussi les coordonnées de ![]()
Finalement nous trouvons que les coordonnées de ![]() sont
sont ![]()
Autrement dit les coordonnées de ![]() sont obtenues par les différences entre les coordonnées de l’extrémité du vecteur, le point
sont obtenues par les différences entre les coordonnées de l’extrémité du vecteur, le point ![]() , et l’origine du vecteur, le point
, et l’origine du vecteur, le point ![]() .
.
Démonstration :
Les coordonnées du vecteur ![]() sont les coordonnées du point
sont les coordonnées du point ![]() , soit
, soit ![]() .
.
On sait que ![]() . Donc les coordonnées du vecteur
. Donc les coordonnées du vecteur ![]() sont
sont ![]() .
.
La relation de Chasles appliqué à ![]() donne :
donne : ![]() .
.
Donc les coordonnées de ![]() sont obtenus en faisant la somme des coordonnées de
sont obtenus en faisant la somme des coordonnées de ![]() et de
et de ![]() , soit
, soit ![]() , c’est-à-dire
, c’est-à-dire ![]() .
.
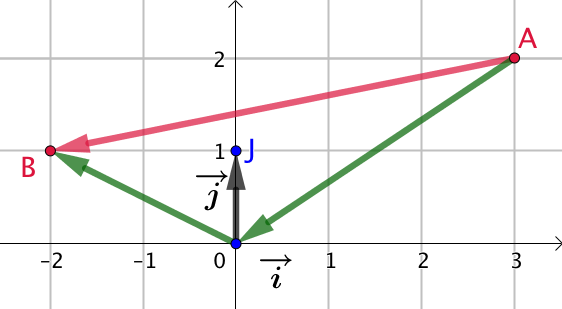 Exemple :
Exemple :
![]() et
et ![]()
On fait la différences entre les coordonnées de ![]() et celles de
et celles de ![]() :
:
- L’abscisse de
 est
est 
- L’ordonnée de
 est
est 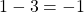
Donc ![]()
Interprétation géométrique : Pour passer du point ![]() au point
au point ![]() , on se déplace « à gauche » de 5 unités, puis on « descend » d’une unité.
, on se déplace « à gauche » de 5 unités, puis on « descend » d’une unité.
Démonstration :
Soient les points ![]() et
et ![]() projetés orthogonaux de
projetés orthogonaux de ![]() sur l’axe des abscisses et l’axe des ordonnées, et soient les points
sur l’axe des abscisses et l’axe des ordonnées, et soient les points ![]() et
et ![]() projetés orthogonaux de
projetés orthogonaux de ![]() sur l’axe des abscisses et l’axe des ordonnées. Soit
sur l’axe des abscisses et l’axe des ordonnées. Soit ![]() le point d’intersection des droites (AK) et (BL).
le point d’intersection des droites (AK) et (BL).
Par construction le triangle ![]() est rectangle en
est rectangle en ![]() .
. ![]() est égale à la distance AB qui vérifie le théorème de Pythagore :
est égale à la distance AB qui vérifie le théorème de Pythagore : ![]() .
.
Nous voyons que ![]() . Nous savons par ailleurs que la distance séparant deux points d’une droite numérique est la valeur absolue de la différence de leurs abscisses.
. Nous savons par ailleurs que la distance séparant deux points d’une droite numérique est la valeur absolue de la différence de leurs abscisses.
Comme ![]() et
et ![]() sont les projetés orthogonaux respectifs de
sont les projetés orthogonaux respectifs de ![]() et
et ![]() sur l’axe des abscisses, leurs abscisses respectives sont
sur l’axe des abscisses, leurs abscisses respectives sont ![]() et
et ![]() . Par conséquent
. Par conséquent ![]() .
.
![]() . On démontre de la même façon que
. On démontre de la même façon que ![]() .
.
Ce qui donne : ![]() .
.
Rappel sur les valeurs absolues : pour tout réel ![]() ,
, ![]() . Donc
. Donc ![]()
Ce qui donne par passage aux racines carrées : ![]() .
.
Démonstration :
Soit le vecteur ![]() de coordonnées
de coordonnées ![]() . On sait qu’il existe un point
. On sait qu’il existe un point ![]() possédant les mêmes coordonnées que
possédant les mêmes coordonnées que ![]() , tel que
, tel que ![]() .
.
D’après la propriété précédente : ![]() .
.
Comme les coordonnées du point ![]() , origine du repère, sont
, origine du repère, sont ![]() et que
et que ![]() , il vient que
, il vient que ![]() .
.
Exemple : soient les vecteurs ![]() et
et ![]() . Leur déterminant est :
. Leur déterminant est : ![]() .
.
Démonstration : Soient deux vecteurs ![]() et
et ![]() .
.
1ère partie : Supposons que les deux vecteurs soient colinéaires.
Alors il existe un nombre réel ![]() tel que
tel que ![]() .
.
Ce qui signifie que ![]() et que
et que ![]() . Donc
. Donc ![]()
2ème partie ( réciproque) : Supposons que ![]() alors
alors ![]() . (1)
. (1)
1er cas : ![]() et
et ![]() . L’égalité (1) devient :
. L’égalité (1) devient : ![]() puis
puis ![]() .
.
On pose ![]() , ce qui donne :
, ce qui donne : ![]() et
et ![]() . Donc
. Donc ![]() . Les deux vecteurs sont colinéaires.
. Les deux vecteurs sont colinéaires.
2ème cas : ![]() . L’égalité (1) devient
. L’égalité (1) devient ![]()
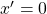 . Alors
. Alors 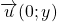 et
et 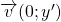 sont colinéaires puisqu’ils ont la même direction verticale.
sont colinéaires puisqu’ils ont la même direction verticale.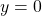 . Alors
. Alors 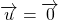 . Tous les vecteurs sont colinéaires au vecteur nul. C’est donc le cas de
. Tous les vecteurs sont colinéaires au vecteur nul. C’est donc le cas de 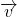 .
.
3ème cas : ![]() . L’égalité (1) devient
. L’égalité (1) devient ![]()
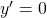 . Alors
. Alors 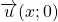 et
et 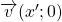 sont colinéaires puisqu’ils ont la même direction horizontale.
sont colinéaires puisqu’ils ont la même direction horizontale.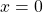 . Alors
. Alors 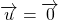 . Tous les vecteurs sont colinéaires au vecteur nul. C’est donc le cas de
. Tous les vecteurs sont colinéaires au vecteur nul. C’est donc le cas de