I – Produit d’un vecteur par un réel
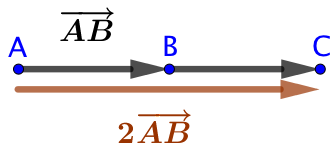 Soient deux points
Soient deux points ![]() et
et ![]() , on s’intéresse au vecteur
, on s’intéresse au vecteur ![]() qui est égal à la somme
qui est égal à la somme ![]() .
.
On constate que le vecteur ![]() a la même direction et le même sens que le vecteur
a la même direction et le même sens que le vecteur ![]() . On observe également que la norme de
. On observe également que la norme de ![]() et le double de celle de
et le double de celle de ![]() .
.
Cela nous autorise à écrire que ![]()
Attention : il ne s’agit pas d’une multiplication entre nombres réels.
- ayant la même direction que
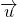 ;
; - dont le sens est celui de
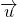 si
si 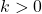 et contraire à celui de
et contraire à celui de 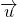 si
si 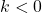 ;
; - dont la norme est égale à
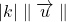 .
.
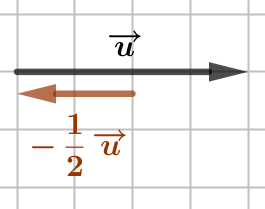 Exemple : Le vecteur
Exemple : Le vecteur ![]() est obtenu en construisant
est obtenu en construisant ![]() puis en divisant la norme par 2.
puis en divisant la norme par 2.
Cas particulier : ![]()
Démonstration :
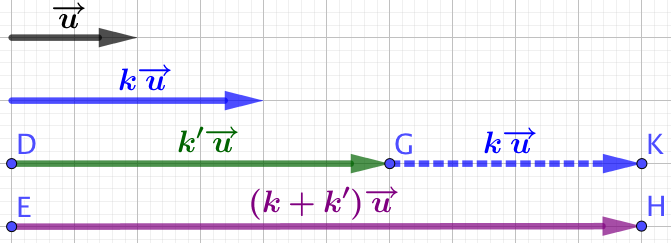
| On considère deux vecteurs On construit la somme de ces deux vecteurs. |
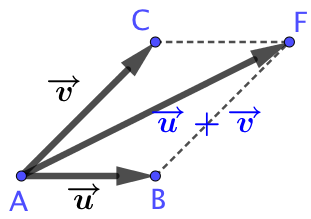 |
| Soit un nombre réel On construit les vecteurs
|
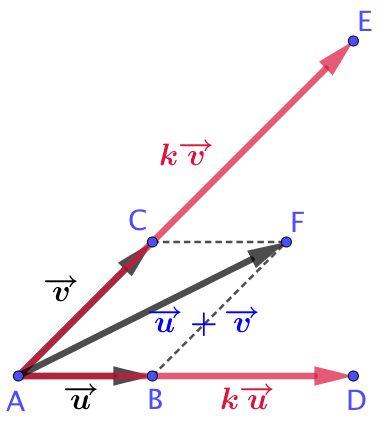 |
| On construit le vecteur
L’objectif est de démontrer que
D’après la réciproque du théorème de Thalès, il vient que : |
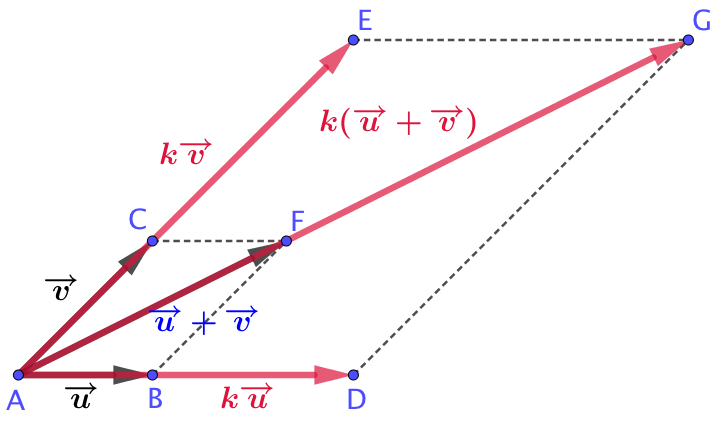 |
![]() car
car ![]() est un parallélogramme puisque
est un parallélogramme puisque ![]()
![]()
![]() et
et ![]() car
car ![]() est un parallélogramme. Comme
est un parallélogramme. Comme ![]() , il vient que
, il vient que ![]()
Puisque ![]() ,
, ![]() et que les vecteurs
et que les vecteurs ![]() et
et ![]() sont dans le même sens, alors
sont dans le même sens, alors ![]() .
.
Relation de Chasles : ![]()
Donc ![]() .
.
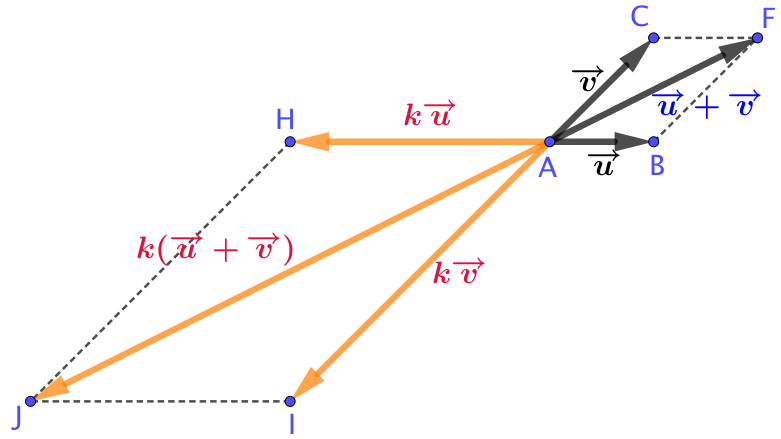 Remarque :
Remarque :
Considérons maintenant un réel ![]() négatif. Alors la figure sera celle de droite.
négatif. Alors la figure sera celle de droite.
La réciproque du théorème Thalès permet à nouveau démontrer la propriété.
Cas particulier : ![]()
La propriété s’écrit : ![]()
Donc .![]()
Ce résultat ressemble à la règle du signe moins devant une parenthèse dans une expression numérique.
 Démonstration dans le cas où
Démonstration dans le cas où ![]() et
et ![]() sont positifs :
sont positifs :
Dans ce cas ![]() ,
, ![]() et
et ![]()
![]()
![]()
On a démontré que les vecteurs ![]() et
et ![]() ont la même norme. Il est par ailleurs évident qu’ils ont le même sens et la même direction que
ont la même norme. Il est par ailleurs évident qu’ils ont le même sens et la même direction que ![]() . Donc ces deux vecteurs sont égaux.
. Donc ces deux vecteurs sont égaux.
Les démonstrations dans les cas ou ![]() et
et ![]() sont de signes opposés ou tous les deux négatifs sont similaires.
sont de signes opposés ou tous les deux négatifs sont similaires.
 Démonstration dans le cas où
Démonstration dans le cas où ![]() et
et ![]() sont positifs :
sont positifs :
Dans ce cas ![]() ,
, ![]() et
et ![]()
![]()
![]()
On a démontré que les vecteurs ![]() et
et ![]() ont la même norme. Il est par ailleurs évident qu’ils ont le même sens et la même direction que
ont la même norme. Il est par ailleurs évident qu’ils ont le même sens et la même direction que ![]() . Donc ces deux vecteurs sont égaux.
. Donc ces deux vecteurs sont égaux.
Les démonstrations dans les cas ou ![]() et
et ![]() sont de signes opposés ou tous les deux négatifs sont similaires.
sont de signes opposés ou tous les deux négatifs sont similaires.
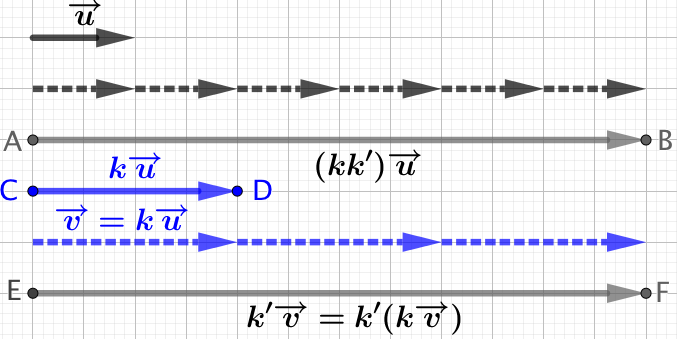
- Pour tout vecteur
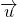 ,
, 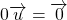
- Pour tout nombre réel
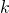 ,
, 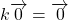
Démonstration de la première propriété :
Puisque ![]() , on peut écrire :
, on peut écrire : ![]()
En développant : ![]() .
.
En ajoutant ![]() au premier membre de l’égalité :
au premier membre de l’égalité : ![]() .
.
En simplifiant par ![]() . il reste :
. il reste : ![]() .
.
Démonstration de la seconde propriété :
Puisque ![]() , on peut écrire :
, on peut écrire : ![]()
En développant : ![]()
En ajoutant ![]() au premier membre de l’égalité :
au premier membre de l’égalité : ![]()
En simplifiant par ![]() . il reste :
. il reste : ![]() .
.
Supposons que ![]() et que de plus
et que de plus ![]() . Montrons alors que nécessairement
. Montrons alors que nécessairement ![]() .
.
Puisque ![]() , on peut multiplier chaque membre de l’égalité par
, on peut multiplier chaque membre de l’égalité par ![]() :
: ![]()
Ce qui donne :![]() . Soit
. Soit ![]() .
.
II – Vecteurs colinéaires
- il existe un réel
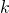 tel que
tel que 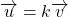 ou
ou - il existe un réel
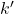 tel que
tel que 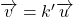
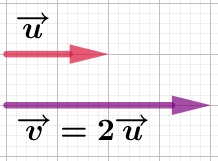 Exemple : Les vecteurs
Exemple : Les vecteurs ![]() et
et ![]() de la figure ci-contre sont colinéaires car :
de la figure ci-contre sont colinéaires car :
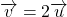
- Mais aussi :
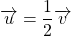
Démonstration : soit ![]() un vecteur quelconque. Puisque
un vecteur quelconque. Puisque ![]() , cela prouve que ces deux vecteurs sont colinéaires.
, cela prouve que ces deux vecteurs sont colinéaires.
Cette propriété découle de la définition du produit d’un vecteur par un nombre réel.
 Démonstration :
Démonstration :
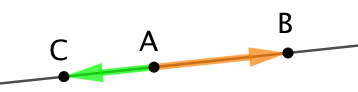
1ère partie : Supposons que les points ![]() ,
, ![]() et
et ![]() sont alignés comme sur la figure ci-contre. Alors les vecteurs
sont alignés comme sur la figure ci-contre. Alors les vecteurs ![]() et
et ![]() , par exemple, sont colinéaires.
, par exemple, sont colinéaires.
2ème partie : supposons que, par exemple, les vecteurs ![]() et
et ![]() soient colinéaires, alors ces deux vecteurs possèdent la même direction.
soient colinéaires, alors ces deux vecteurs possèdent la même direction.
Par conséquent, les droites ![]() et
et ![]() sont parallèles. Comme elles possèdent un point commun
sont parallèles. Comme elles possèdent un point commun ![]() , elles sont confondues. Ce qui achève de démontrer que les points
, elles sont confondues. Ce qui achève de démontrer que les points ![]() ,
, ![]() et
et ![]() sont alignés.
sont alignés.
 Démonstration :
Démonstration :
Supposons que les droites ![]() et
et ![]() soient parallèles. Alors les deux vecteurs
soient parallèles. Alors les deux vecteurs ![]() et
et ![]() sont colinéaires.
sont colinéaires.
Supposons à présents que les vecteurs ![]() et
et ![]() soient colinéaires, alors ils ont la même direction, donc les droites
soient colinéaires, alors ils ont la même direction, donc les droites ![]() et
et ![]() sont parallèles.
sont parallèles.
