I – Définition
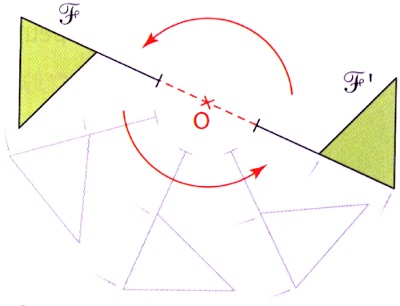 Exemple : En faisant accomplir autour du point O un demi-tour à la figure
Exemple : En faisant accomplir autour du point O un demi-tour à la figure ![]() , celle-ci se superpose exactement à la figure
, celle-ci se superpose exactement à la figure ![]() .
.
Bien évidemment, en faisant accomplir autour du point un demi-tour à la figure ![]() , celle-ci se superpose exactement à la figure
, celle-ci se superpose exactement à la figure ![]() .
.
Les figures ![]() et
et ![]() sont symétriques par rapport au point O.
sont symétriques par rapport au point O.
Le point O est le centre de la symétrie qui transforme la figure ![]() en
en ![]() .
.
II Symétrique d’un point
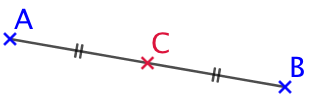 Deux points A et B sont symétriques par rapport au point C si et seulement si le point C est le milieu du segment [AB]. Les phrases suivantes sont équivalentes :
Deux points A et B sont symétriques par rapport au point C si et seulement si le point C est le milieu du segment [AB]. Les phrases suivantes sont équivalentes :
- A et B sont symétriques par rapport à C.
- Le symétrique de A par rapport à C est B.
- Le symétrique de B par rapport à C est A.
Construction du symétrique d’un point
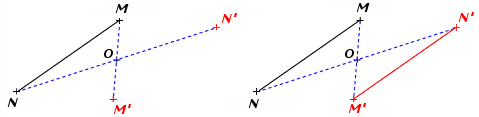
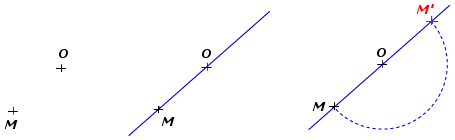 Pour tracer le symétrique M’ de M par rapport à O :
Pour tracer le symétrique M’ de M par rapport à O :
- On trace à la règle la droite (MO);
- On trace un demi-cercle de centre O qui passe par M
- Ce demi-cercle coupe la droite (MO) au point M’, symétrique de M par rapport à O.
III – Symétrique d’une droite
Construction du symétrique d’une droite
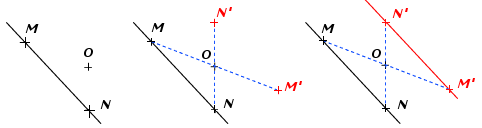 Pour tracer le symétrique d’une droite par rapport au O :
Pour tracer le symétrique d’une droite par rapport au O :
- On choisit deux points de cette droite, par exemple M et N.
- On construit les symétriques des points M et N par rapport à O : M’ et N’
- On trace la droite qui passe par M’ et N’. C’est la droite symétrique de la droite (MN).
IV – Symétrique d’un segment
Construction du symétrique d’un segment
 Pour tracer le symétrique d’un segment [MN] par rapport au O :
Pour tracer le symétrique d’un segment [MN] par rapport au O :
- On construit les symétriques des points M et N par rapport à O : M’ et N’.
- Le segment [M’N’] est l’image du segment [MN] par rapport à O.
Construction du symétrique d’un polygone
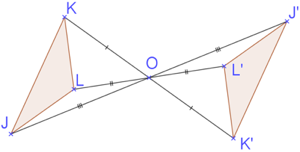
Un polygone est formé de plusieurs segments. Il suffit de construire le symétrique de chaque segment comme vu précédemment. On obtient un polygone de même forme et de même mesure.
Exemple : Le symétrique du triangle JKL par rapport à O est le triangle J’K’L’.
V – Symétrie d’un cercle
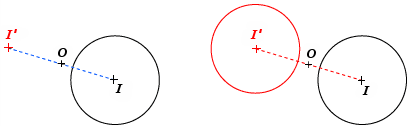 Pour tracer le symétrique du cercle de centre I :
Pour tracer le symétrique du cercle de centre I :
- On construit le symétrique de I par rapport à O : I’.
- On tracer le cercle de centre O et de même rayon.
VI – Centre de symétrie
 Exemples :
Exemples :
- Le milieu d’un segment est le centre de symétrie de ce segment.
- Le centre d’un cercle est le centre de symétrie de ce cercle.
- Le point d’intersection des diagonales d’une rectangle est le centre de symétrie de ce rectangle.
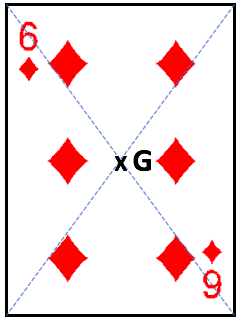
- La carte du 6 de carreau possède un centre de symétrie qui est le point G.
ATTENTION : une figure peut ne pas avoir de centre de symétrie, comme par exemple, un triangle.
