I – Introduction
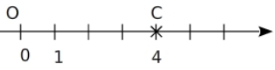 En sixième nous avons appris à placer des nombres sur une demi-droite graduée comme ceci : L’origine est le point d’abscisse 0 et l’abscisse du point C est le nombre 4.
En sixième nous avons appris à placer des nombres sur une demi-droite graduée comme ceci : L’origine est le point d’abscisse 0 et l’abscisse du point C est le nombre 4.
En cinquième on va aussi s’intéresser à ce qu’il se passe à gauche de l’origine. On va s’intéresser à la droite entière et pas uniquement à la demi-droite.
Les abscisses des points à droite de l’origine seront appelées les nombres positifs et les abscisses des points à gauche de l’origine seront appelées les nombres négatifs.
- Les nombres supérieurs ou égaux à 0 sont appelés les nombres positifs.
- Les nombres inférieurs ou égaux à 0 sont appelés les nombres négatifs.
- 0 est considéré à la fois comme un nombre positif et un nombre négatif.
- Les nombres positifs et les nombres négatifs forment l’ensemble des nombres relatifs.
- Un nombre positif s’écrit avec un signe
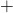 mais ce signe n’est pas obligatoire
mais ce signe n’est pas obligatoire - Un nombre négatif s’écrit toujours avec un signe
 .
.
Exemples :
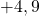 ou
ou 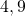 est un nombre positif.
est un nombre positif.  est un nombre positif.
est un nombre positif.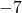 est un nombre négatif.
est un nombre négatif. 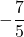 est un nombre positif.
est un nombre positif.
II – Repérage sur une droite
- un point O appelé origine de la droite graduée ;
- une unité.
- Tout point d’une droite graduée peut être repéré par un nombre relatif appelé son abscisse.
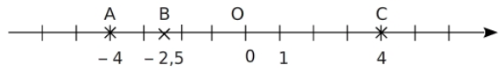 Exemple :
Exemple :
- L’abscisse de l’origine O est le nombre 0.
- Les points A, B et C ont pour abscisses respectives
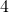 ;
; 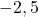 et
et 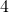 .
.
On note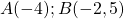 et
et 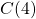 .
.
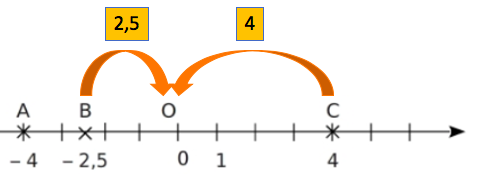 Exemple :
Exemple :
La distance à zéro du nombre ![]() est la distance OB car B a pour abscisse
est la distance OB car B a pour abscisse ![]() .
.
Elle vaut donc 2,5.
La distance à zéro du nombre ![]() est la distance OC. Elle est donc égale à 4.
est la distance OC. Elle est donc égale à 4.
Exemple : les nombres ![]() et
et ![]() ont la même distance à zéro. ils sont opposés.
ont la même distance à zéro. ils sont opposés.
Exemple : les points ![]() et C(4) sont bien symétriques par rapport à l’origine car ils ont la même distance à zéro qui vaut 4 et leurs abscisses sont de signe opposé.
et C(4) sont bien symétriques par rapport à l’origine car ils ont la même distance à zéro qui vaut 4 et leurs abscisses sont de signe opposé.
III – Comparaison de nombres relatifs
- Deux nombres relatifs positifs sont rangés dans l’ordre de leur distance à zéro.
- Un nombre relatif négatif est toujours inférieur à un nombre relatif positif.
- Deux nombres relatifs négatifs sont rangés dans l’ordre inverse de leur distance à zéro.

Exemple : ![]()
IV – Addition de deux nombres relatifs
- Pour additionner deux nombres relatifs de même signe, on additionne leur distance à zéro et on garde le signe commun.
- Pour additionner deux nombres relatifs de signes contraires, on soustrait leur distance à zéro et le signe du résultat est le signe de celui qui a la plus grande distance à zéro.
- La somme de deux nombres opposés est égale à 0.
Exemple : On veut calculer ![]() .
.
- La distance à zéro de
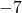 est
est 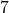
- La distance à zéro de
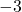 est
est 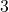
- La somme des distances à zéro est :
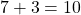 .
. - On rajoute le signe commun :
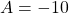
Remarque : La somme de deux nombres négatifs est un nombre négatif.
![]() . C’est l’addition de deux nombres telle que nous la connaissions en classe de sixième.
. C’est l’addition de deux nombres telle que nous la connaissions en classe de sixième.
Exemple : On veut calculer ![]() .
.
- La distance à zéro de
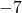 est
est 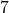
- La distance à zéro de
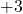 est
est 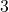 . C’est donc
. C’est donc 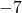 qui a la plus grande distance à zéro.
qui a la plus grande distance à zéro. - La soustraction de leur distance à zéro est :
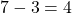 .
. - On ajoute le signe de celui qui a la plus grande distance à zéro :
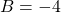
Exemple : ![]() car les deux nombres sont oposés.
car les deux nombres sont oposés.
On peut aussi commencer par regrouper des termes opposés s’il y en a.
Exemple : On veut calculer ![]()
- La somme des deux nombres positifs est :
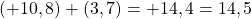
- La somme des deux nombres négatifs est :
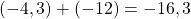
- Donc
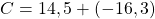
- La distance à zéro de
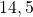 est
est 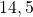
- La distance à zéro de
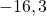 est
est 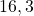 . C’est donc
. C’est donc 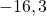 qui a la plus grande distance à zéro.
qui a la plus grande distance à zéro. - La soustraction de leur distance à zéro est :
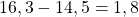 .
. - Finalement
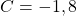
V – Repérage dans le plan
 Pour se repérer sur une carte, on utilise souvent les points cardinaux : nord, ouest, sud et est. La droite ouest-est et la droite sud-nord sont perpendiculaires.
Pour se repérer sur une carte, on utilise souvent les points cardinaux : nord, ouest, sud et est. La droite ouest-est et la droite sud-nord sont perpendiculaires.
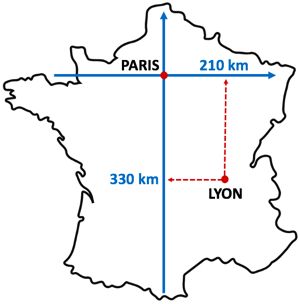
On peut ensuite choisir Paris comme point de départ de notre voyage. Alors la ville de Lyon se situe au sud-est de la ville de Paris et la ville de Brest se situe à l’ouest de Paris.
Enfin, pour être plus précis, on choisit une unité de longueur, par exemple le kilomètre. On peut alors repérer que Lyon se situe à environ 210 km à l’est de Paris et à 330 km au sud de Paris.
 Exemples :
Exemples :
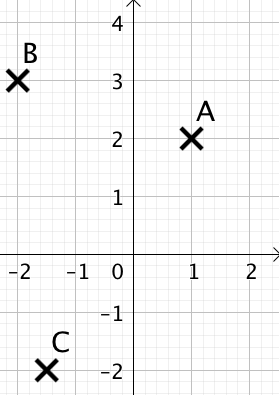
Les coordonnées du point ![]() sont : 1 pour l’abscisse et 2 pour l’ordonnée. On note :
sont : 1 pour l’abscisse et 2 pour l’ordonnée. On note : ![]() en commençant par l’abscisse.
en commençant par l’abscisse.
Pour les deux autres points : ![]() et
et ![]() .
.
Le point O, origine du repère a comme coordonnées ![]() .
.
