I – Sous-multiples de l’unité
1) Les dixièmes
Quand on coupe une unité en 10 parties égales, on obtient des dixièmes.
Un dixième se note : 
. Dans l’unité, il y a 10 dixièmes donc : 
.
Exemples :
 |
 |
 |
 |
 |
 |
2) Les centièmes
Quand on coupe une unité en 100 parties égales, on obtient des centièmes.
Un centième se note : 
. Dans l’unité, il y a 100 centièmes donc : 
.
Exemples :
 |
 |
 |
|
 |
|
3) Les millièmes
Quand on coupe une unité en 1000 parties égales, on obtient des millièmes.
Un millième se note : 
. Dans l’unité, il y a 1000 millièmes donc : 
.
Exemple :
On se rappelle que : 
![\[ \dfrac{14 \: 531}{1000} = {14 \: 531} \times \dfrac{1}{1000} = {14 \: 000} \times \dfrac{1}{1000} + 500 \times \dfrac{1}{1000} + 31 \times \dfrac{1}{1000} +1 \times \dfrac{1}{1000} = 14,531\]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-44b2046da22503ddcfc49264dc5092ec_l3.png "Rendered by QuickLaTeX.com")
II – Décomposition et noms des chiffres
Il peut aussi se noter en utilisant une virgule, c’est son écriture décimale qui est composée d’une partie entière et d’une partie décimale.
Exemple : On considère le nombre décimal 1 345,824.
On peut utiliser un tableau pour représenter ce nombre :
Ce nombre peut se lire de trois manières différentes :
- mille-trois-cent-quarante-cinq unités et huit−cent−vingt−quatre millièmes
- mille-trois-cent-quarante-cinq unités et huit dixièmes deux centièmes quatre millièmes
- mille-trois-cent-quarante-cinq unités virgule huit−cent−vingt−quatre
Il peut se décomposer ainsi :
![\[ {1 \: 345,824} = (1 \times 1000) + (3 \times 100) + (4 \times 10) + (5 \times 1) + \left ( 8 \times \dfrac{1}{10} \right ) + \left ( 2 \times \dfrac{1}{100} \right ) + \left ( 4 \times \dfrac{1}{1000} \right ) \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-912f8604e15b5821a3348d1c4764abd9_l3.png "Rendered by QuickLaTeX.com")
Voici le nom de chaque chiffre :
- 1 est le chiffre des unités des milliers
- 3 est le chiffre des centaines
- 4 est le chiffre des dizaines
- 5 est le chiffre des unités
- 8 est le chiffre des dixièmes
- 2 est le chiffre des centièmes
- 4 est le chiffre des millièmes
Exemples :
![\[ 3,14 = \dfrac{314}{100} \qquad 0,5 = \dfrac{1}{2} \qquad 0,75 = \dfrac{3}{4} \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-cac6719f2addf721efc05cfc31fa70d7_l3.png "Rendered by QuickLaTeX.com")
Exemple : 2,36 = 2,360 car 6 centièmes sont égaux à 60 millièmes.
Habitude : il existe une situation de la vie courante ou nous conservons le dernier zéro d’un nombre décimal : lorsque nous parlons de prix. On dira que cette paire de chaussettes coûte 3,50 € (3 euros 50) au lieu de 3,5 €. Cela s’explique par le fait que nous comptons les petits montants d’argent en centimes d’euros (qui sont des centièmes d’euros) et non en dixièmes d’euros.
- 25 peut s’écrire avec une virgule : 25,0
- 25 peut s’écrire sous la forme d’une fraction décimale :
.
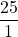III – Repérage sur une demi-droite graduée
Exemple : Quelles sont les abscisses des points A et B ?
Une unité est divisée en dix parts égales, ce qui signifie qu’elle est partagée en dix dixièmes.
Le point A se trouve 2 dixièmes après 3, donc son abscisse est 
.
Le point B se trouve 3 dixièmes après l’origine du repère O, donc son abscisse est 
.
On note A(3,2) et B(0,3).
IV – Comparaison et rangement
1) – Comparaison de deux nombres décimaux
- on compare les parties entières ;
- si les parties entières sont égales alors on compare les chiffres des dixièmes ;
- si les chiffres des dixièmes sont égaux alors on compare les chiffres des centièmes ;
- et ainsi de suite jusqu’à ce que les deux nombres aient des chiffres différents.
Exemple : On veut comparer les nombres 81,357 et 81,36.
- On compare d’abord les parties entières des deux nombres ;
- elles sont égales donc on compare les chiffres des dixièmes ;
- ils sont égaux donc on compare les chiffres des centièmes ;
- 5 < 6 donc 81,357 < 81,36.
Autre méthode :
Dans le cas où deux nombres ont la même partie entière, on compare leur partie décimale. Pour comparer les parties décimales sans faire d’erreur, il faut que celles-ci possèdent le même nombre de chiffres. Si l’une en possède moins que l’autre, on lui ajoute autant de zéros que nécessaire.
Pour comparer 81,357 et 81,36, on compare 357 avec 360, après avoir ajouté un zéro à 36. On constate alors que 357 < 360 donc que 81,357 < 81,36.
Vidéo : Comparer deux nombres |
2) Rangement de nombres décimaux
Exemple : Pour ranger les nombres 25,342 ; 253,42 ; 25,243 ; 235,42 ; 25,324 dans l’ordre croissant, on repère le plus petit puis le plus petit des nombres qui restent et ainsi de suite jusqu’au dernier.
On obtient donc : 25,243 < 25,324 < 25,342 < 235,42 < 253,42.
Vidéo : ranger du plus petit au plus grand |
V – Ordre de grandeur
1) Ordre de grandeur d’un nombre
Remarque : Calculer un ordre de grandeur permet de vérifier plus facilement la cohérence d’un résultat, c’est-à-dire que ce résultat est logique par rapport à l’énoncé du problème.
Exemple : La superficie de la France métropolitaine est de 551 695 km2. Un ordre de grandeur de cette superficie est de 550 000 km2. Cet ordre de ordre de grandeur n’est pas la valeur exacte de la superficie de la France métropolitaine mais est une valeur suffisamment proche pour être utilisée dans des calculs.
Exemple : On veut déterminer un ordre de grandeur du calcul suivant : 546,3 + 52.
On cherche un ordre de grandeur de chaque terme qu’on utilise dans le calcul.
550 est proche de 546,3 et 50 est proche de 52. Comme 550 + 50 = 600, la somme 546,3 + 52 est proche de 600. On dit que 600 est un ordre de grandeur de 546,3 + 52.
Exemple : veut déterminer un ordre de grandeur du calcul suivant : 65,7 × 4,1
On cherche un ordre de grandeur de chaque facteur qu’on utilise dans le calcul.
65,7 est proche de 65 et 4,1 est proche de 4. Comme 65 × 4 = 260, le produit 65,7 × 4,1 est proche de 260. 260 est donc un ordre de grandeur de 65,7 × 4,1.
Vidéo : ordre de grandeur |
2) Encadrement d’un nombre décimal
Exemples :
- 2,4 est encadré par 2 et par 3 car 2 < 2,4 < 3
- 3,141 est encadré par 3,14 et par 3,15 car 3,14 < 3,141 < 3,15
- Encadrement à l’unité : la différence entre le plus grand et le plus petit vaut 1.
- Encadrement au dixième : la différence entre le plus grand et le plus petit vaut 0,1.
- Encadrement au centième : la différence entre le plus grand et le plus petit vaut 0,01.
- Encadrement au millième : la différence entre le plus grand et le plus petit vaut 0,001.
- etc …
Exemples :
- Encadrement à l’unité : 2 < 2,4 < 3
- Encadrement au centième : 3,14 < 3,141 < 3,15
Exemple : entre 9,81 et 9,82, je peux intercaler 9,813 car : 9,81 < 9,813 < 9,8.
Video : encadrer un nombre |
