I – Vocabulaire

Étymologie latine :
- Numérateur : numerator, qui signifie « celui qui compte ». Pour une fraction, cela peut se traduire par : « combien de morceaux on va prendre lors d’un partage.
- Dénominateur : denominator, qui signifie « celui qui désigne », c’est donc celui qui décide, celui qui indique « par combien on partage ».
ATTENTION :
- Le numérateur et le dénominateurs sont des nombres entiers (pas de virgule)
- Le dénominateur d’une fraction ne doit jamais être égal à zéro.
II – Lecture d’une fraction
Exemples : ![]() se lit quatre septièmes et
se lit quatre septièmes et ![]() se lit trois dixièmes.
se lit trois dixièmes.
Mais il existe des exceptions :
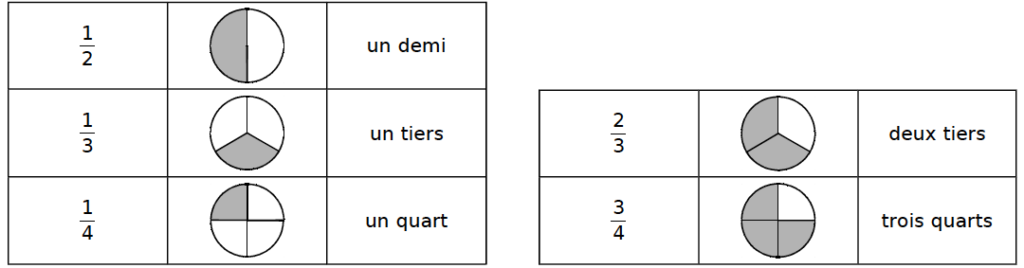
III – Fraction et partage
Exemple : Colorier les deux sixièmes d’un disque :
| On partage le disque en six parts égales : Chaque part représente |
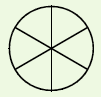 |
| On colorie deux parts sur les six. La partie colorée est constituée de deux parts de |
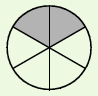 |
IV – Quotient sous la forme d’une fraction
C’est-à-dire que ![]() .
.
On dit également que ![]() est le nombre qui, multiplié par
est le nombre qui, multiplié par ![]() , donne
, donne ![]() . Soit
. Soit ![]() .
.
| 1 unité est représentée par : | |
| 4 unités sont représentées par : | |
![]() est le nombre tel que
est le nombre tel que ![]() , soit le nombre tel que
, soit le nombre tel que ![]()
Exemple : ![]() .
.
V – Comparaison d’une fraction à 1
- Si le numérateur est inférieur au dénominateur alors la fraction est inférieure à 1.
- Si le numérateur et le dénominateur sont égaux alors la fraction est égale à 1.
- Si le numérateur est supérieur au dénominateur alors la fraction est supérieure à 1.
Exemple : Comment comparer les fractions ![]() et
et ![]() à 1 ?
à 1 ?
![]() est inférieure à 1 car le numérateur 11 est inférieur au dénominateur 15.
est inférieure à 1 car le numérateur 11 est inférieur au dénominateur 15.
![]() est égale à 1 car le numérateur 15 est égal au dénominateur 15.
est égale à 1 car le numérateur 15 est égal au dénominateur 15.
![]() est supérieure à 1 car le numérateur 17 est supérieur au dénominateur 15.
est supérieure à 1 car le numérateur 17 est supérieur au dénominateur 15.
VI – Encadrement d’une fraction entre deux nombres entiers consécutifs
Exemple : Pour encadrer la fraction ![]() entre deux entiers consécutifs.
entre deux entiers consécutifs.
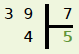 On effectue la division euclidienne de 39 par 7 : 39 = 5 x 7 + 4.
On effectue la division euclidienne de 39 par 7 : 39 = 5 x 7 + 4.
5 est la valeur approchée à l’unité par défaut de la fraction ![]() .
.
Donc ![]() , soit
, soit ![]()
VII – Décomposition d’une fraction
Exemple : Pour décomposer la fraction ![]() en somme d’un nombre entier et d’une fraction inférieure à 1 :
en somme d’un nombre entier et d’une fraction inférieure à 1 :
On sait déjà que 39 = 5 x 7 + 4. Donc ![]() . On vérifie bien que
. On vérifie bien que ![]() .
.
Remarque : On utilise les symboles > pour « plus grand que » et < pour « plus petit que ».
VIII – Fraction et demi-droite graduée
Exemple : Sur une demi-droite graduée, on veut placer les points A et B d’abscisses respectives ![]() et
et ![]() .
.
On commence par on choisir une unité de longueur que l’on partage en six parts égales. Chacune de ces parts correspond donc à ![]() de de l’unité.
de de l’unité.
Pour placer le point A, on remarque que ![]() . Donc on reporte cinq sixièmes à partir du point O.
. Donc on reporte cinq sixièmes à partir du point O.
Pour placer le point B, on décompose la fraction ![]() en faisant la division euclidienne de 22 par 6.
en faisant la division euclidienne de 22 par 6.
On obtient ![]() . Donc on reporte quatre sixièmes après 3.
. Donc on reporte quatre sixièmes après 3.
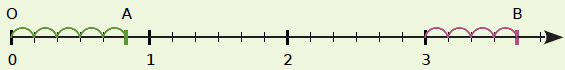
IX – Pourcentages
Les pourcentages sont très utiles pour exprimer des proportions, des augmentations ou des diminutions. On les rencontre partout : pourcentage de globules blancs dans le sang, sondages d’opinion, pourcentage de chômage, pourcentage de gaz carbonique dans l’atmosphère, pourcentage de services gagnants au tennis,… Vous en aurez souvent besoin.
1) Calcul à partir d’un pourcentage
Exemple : 36 % des 425 élèves d’un collège sont externes. Combien y a-t-il d’élèves externes ?
Pour calculer le nombre d’externes, on calcule 36 % de 425 en deux étapes :
- On calcule le produit de 36 et de 425 :
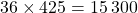
- On divise ce produit par 100:
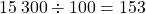
2) Pourcentages particuliers
- Prendre 10 % d’un nombre, c’est en prendre le dixième.
- Prendre 50 % d’un nombre, c’est en prendre la moitié.
- Prendre 25 % d’un nombre, c’est en prendre le quart.
- Prendre 75 % d’un nombre, c’est en prendre les trois quarts.
- Prendre 100 % d’un nombre, c’est en prendre la totalité.
X – Addition de fractions de même dénominateur
- le numérateur est la somme des numérateurs des deux fractions ;
- le dénominateur est le dénominateur commun aux deux fractions.
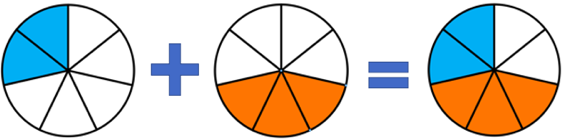 Exemple :
Exemple : ![]()
