I – Quotient

Le quotient ![]() est le résultat exact de la division de
est le résultat exact de la division de ![]() par
par ![]() . C’est le nombre qui, multiplié par
. C’est le nombre qui, multiplié par ![]() , donne
, donne ![]() . Soit
. Soit ![]() .
.
Exemples :
- Tout nombre décimal
 peut d’écrire sous la forme d’un quotient. En effet
peut d’écrire sous la forme d’un quotient. En effet 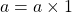 donc
donc 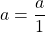 .
. - Le quotient de la division de
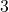 par
par 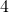 s’écrit
s’écrit  . Ce quotient vérifie l’égalité :
. Ce quotient vérifie l’égalité : 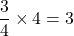 . En effet nous savons que
. En effet nous savons que 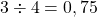 et que
et que 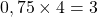 . Dans cet exemple
. Dans cet exemple  est le nombre décimal
est le nombre décimal 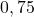 .
. - Le quotient de la division de
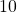 par
par 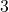 s’écrit
s’écrit 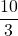 . Ce quotient vérifie l’égalité :
. Ce quotient vérifie l’égalité : 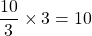 . Par contre le résultat de la division de 10 par 3 ne tombe pas juste. Dans cet exemple
. Par contre le résultat de la division de 10 par 3 ne tombe pas juste. Dans cet exemple 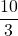 n’est pas un nombre décimal. Une valeur approchée de
n’est pas un nombre décimal. Une valeur approchée de 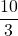 est
est 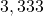 .
.
II – Quotients égaux
Soient ![]() ,
, ![]() et
et ![]() des nombres, avec
des nombres, avec ![]() et
et ![]() .
.
- Un quotient ne change pas quand on multiplie son numérateur et son dénominateur par un même nombre non nul :
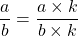
- Un quotient ne change pas quand on divise son numérateur et son dénominateur par un même nombre non nul :
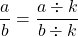
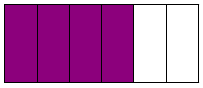
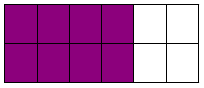
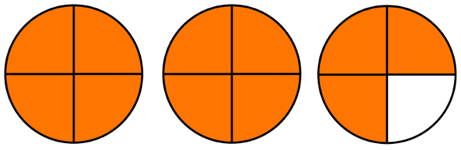
Exemple : Les aires des trois surfaces coloriées sont égales. Elles correspondent à trois quotient qui sont égaux.
 |
 |
 |
Démonstration :
Première partie : D’après la définition du quotient de ![]() par
par ![]() , on sait que
, on sait que ![]() est le nombre qui multiplié à
est le nombre qui multiplié à ![]() donne
donne ![]() :
: ![]() .
.
Faisons le calcul suivant : ![]() . Cela signifie que
. Cela signifie que ![]() est le nombre qui multiplié à
est le nombre qui multiplié à ![]() donne
donne ![]() .
.
Conclusion : ![]()
Deuxième partie : En utilisant le résultat de la première partie, on peut écrire l’égalité suivante : ![]() .
.
Or ![]() et
et ![]() .
.
Donc ![]() .
.
III – Fraction et proportion
Exemple : ![]() est un quotient.
est un quotient. ![]() est une fraction.
est une fraction.
Il faut savoir passer d’une fraction à un nombre décimal et vis-versa.
Exemples :
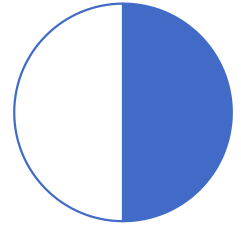
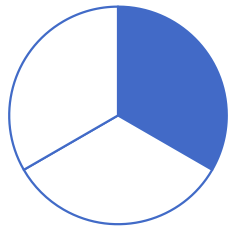
Remarque : Une fraction représente aussi une proportion, une partie d’un tout. Nous découpons une tarte pour en manger une partie (en bleu ci-dessous). La fraction représente la partie colorée.
 |
 |
 |
 |
| Une demi-tarte : |
Un tiers de tarte : |
Un quart de tarte : |
Deux cinquièmes de tarte : |
Exemple : Dans un groupe de 11 personnes, 4 portent des lunettes. La proportion de porteurs de lunettes au sein de ce groupe sera donnée par la fraction : ![]()
IV – Simplification de fraction
Une fraction que l’on ne peut plus simplifier est dite irréductible.
- On décompose le numérateur en facteurs premiers ;
- On décompose le dénominateur en facteurs premiers ;
- On utilise la propriété des quotients égaux :
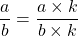
Exemple : On va simplifier la fraction ![]()
- On décompose le numérateur en facteurs premiers :
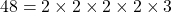
- On décompose le dénominateur en facteurs premiers :
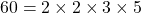
- On utilise la propriété des quotients égaux :
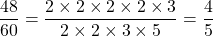
![]() n’est plus simplifiable, elle est donc irréductible. C’est la fraction la plus simple égale à
n’est plus simplifiable, elle est donc irréductible. C’est la fraction la plus simple égale à ![]() .
.
Application à la division : On veut connaître le résultat de la division de 9 par 0,4 sans avoir à poser cette division.
![]()
V – Fractions décimales
Exemple : ![]() est une fraction décimale.
est une fraction décimale.
Exemple : ![]() .
.
VI – Pourcentage
Les pourcentages sont très utiles pour exprimer des proportions, des augmentations ou des diminutions. On les rencontre partout : pourcentage de globules blancs dans le sang, sondages d’opinion, pourcentage de chômage, pourcentage de gaz carbonique dans l’atmosphère, pourcentage de services gagnants au tennis,… Vous en aurez souvent besoin.
1) Calcul d’un pourcentage
Exemple : Une ville compte 25 000 électeurs. Le vainqueur des dernières élections municipales a obtenu 13 500 voix. Quel est le pourcentage des électeurs de cette ville qui ont voté pour ce candidat ?
La proportion recherchée est : ![]() . Conclusion : 54% des habitants de cette ville ont voté pour le gagnant.
. Conclusion : 54% des habitants de cette ville ont voté pour le gagnant.
2) Calcul à partir d’un pourcentage
Exemple : 36 % des 425 élèves d’un collège sont externes. Combien y a-t-il d’élèves externes ?
Pour calculer le nombre d’externes, on calcule 36 % de 425 : ![]() . Il y a donc 153 élèves externes dans ce collège.
. Il y a donc 153 élèves externes dans ce collège.
3) Pourcentages particuliers
Prendre 10 % d’un nombre, c’est en prendre le dixième. Car ![]() .
.
Prendre 50 % d’un nombre, c’est en prendre la moitié. Car ![]() .
.
Prendre 25 % d’un nombre, c’est en prendre le quart. Car ![]() .
.
Prendre 75 % d’un nombre, c’est en prendre les trois quarts. Car ![]() .
.
Prendre 100 % d’un nombre, c’est en prendre la totalité. Car ![]() .
.
VII – Comparaison de fractions
- Si le numérateur est plus grand que le dénominateur, la fraction est supérieure à 1
Explication :
- Si on divise un nombre par un nombre plus petit que lui, le quotient sera plus grand que 1.
- Si on divise un nombre par lui-même, le quotient vaut 1 car
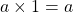 .
. - Si on divise un nombre par un nombre plus grand que lui, le quotient sera plus petit que 1.
Exemples :
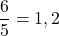 et on sait que
et on sait que 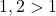
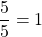
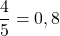 et on sait que
et on sait que 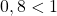
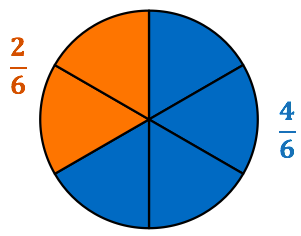 Exemple : Si deux personnes partagent une tarte en 6 parts égales et que l’une d’entre elles mange 4 parts, il en restera 2 pour l’autre personnes. La première personne aura mangé
Exemple : Si deux personnes partagent une tarte en 6 parts égales et que l’une d’entre elles mange 4 parts, il en restera 2 pour l’autre personnes. La première personne aura mangé ![]() de la tarte et l’autre personne mangera que
de la tarte et l’autre personne mangera que ![]() de le tarte.
de le tarte.
On devine facilement qui en a eu le plus : ![]()
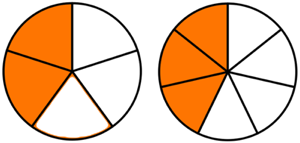
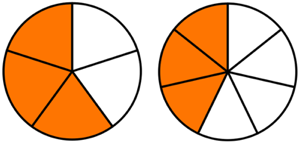 Exemple :
Exemple :
- À gauche, une tarte est divisée en cinq parts égales. Les parts oranges représentent
 de la tarte entière.
de la tarte entière. - À droite, La même tarte est divisée en sept parts égales. Les parts oranges représentent
 de la tarte entière.
de la tarte entière. - On comprend bien que
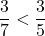
 Exemple : Nous voulons comparer
Exemple : Nous voulons comparer ![]() et
et ![]() .
.
La comparaison graphique ne permet pas d’être certain de la réponse.
![]() et
et ![]()
Puis que ![]() , on en conclut que
, on en conclut que ![]()
VIII – Décomposition d’une fraction supérieure à 1
 Exemple : J’organise une fête. Nous nous retrouvons à 11 personnes. Chacune mange un quart de pizza. Cela fait 11 quarts de pizza à acheter.
Exemple : J’organise une fête. Nous nous retrouvons à 11 personnes. Chacune mange un quart de pizza. Cela fait 11 quarts de pizza à acheter.
Comme ![]() , le commerçant me vend 3 pizzas entières et 3 parts de pizza. Car 11 quarts de pizza sont équivalents à 2 pizzas entières + 3 quarts de pizza.
, le commerçant me vend 3 pizzas entières et 3 parts de pizza. Car 11 quarts de pizza sont équivalents à 2 pizzas entières + 3 quarts de pizza.
En langage mathématique, cela s’écrit : ![]() . On a ainsi décomposé une fraction supérieure à 1 en une somme d’un nombre entier et d’une fraction inférieure à 1.
. On a ainsi décomposé une fraction supérieure à 1 en une somme d’un nombre entier et d’une fraction inférieure à 1.
La méthode de décomposition d’une fraction ![]() supérieure à 1 est la suivante :
supérieure à 1 est la suivante :
- On fait la division euclidienne du numérateur
 par le dénominateur
par le dénominateur 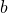 :
: 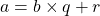 , où
, où  est le quotient et
est le quotient et  le reste inférieur à
le reste inférieur à 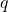 .
. - On écrit que
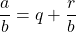
Exemple : On va décomposer la fraction ![]() . La division euclidienne de
. La division euclidienne de ![]() par
par ![]() donne :
donne : ![]() . Ce qui donne la décomposition :
. Ce qui donne la décomposition : ![]()
Utilisation de la décomposition : comparaison d’un nombre avec une fraction
On veut comparer ![]() et
et ![]() . On a vu précédemment que
. On a vu précédemment que ![]() . La question est de comparer
. La question est de comparer ![]() et
et ![]() .
.
On sait d’une part que ![]() et que
et que ![]() . Donc nécessairement
. Donc nécessairement ![]() .
.
IX – Somme et soustraction de fractions
1) Somme et soustraction de deux fractions ayant le même dénominateur
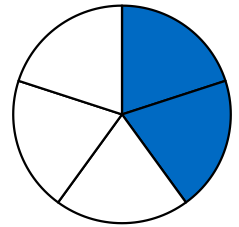
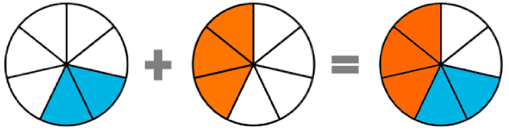 Exemple : La figure de droite nous montre que
Exemple : La figure de droite nous montre que ![]() .
.
On comprend aussi le résultat suivant : ![]() .
.
![]()
2) Somme et soustraction de fractions dont le dénominateur de l’une est le multiple du dénominateur de l’autre
Exemple : On veut faire la somme de ![]() et de
et de ![]() . Les dénominateurs étant différents, on ne peut pas utiliser la propriété précédente.
. Les dénominateurs étant différents, on ne peut pas utiliser la propriété précédente.
Par contre, on remarque que le dénominateur de ![]() est le double de celui de
est le double de celui de ![]() . Mais :
. Mais : ![]() .
.
Donc ![]()
