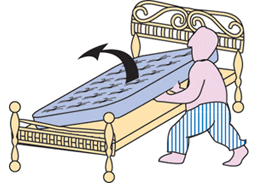
 Les fabricants de lits recommandent de retourner votre matelas périodiquement afin de le conserver dans un bon état le plus longtemps possible. Comment êtes-vous censé le retourner pour obtenir une usure minimale ?
Les fabricants de lits recommandent de retourner votre matelas périodiquement afin de le conserver dans un bon état le plus longtemps possible. Comment êtes-vous censé le retourner pour obtenir une usure minimale ?
On va faire appel à la théorie des groupes, le « groupe » en question ici est un ensemble d’actions mathématiques : toutes les façons possibles de retourner, de faire pivoter ou de renverser le matelas pour qu’il s’adapte parfaitement au cadre du lit.
La théorie des groupes est l’une des parties les plus polyvalentes des mathématiques. Elle sous-tend tout, de la chorégraphie de la contredanse et des lois fondamentales de la physique des particules, aux mosaïques de l’Alhambra.
Comme le suggèrent ces exemples, la théorie des groupes fait le pont entre les arts et les sciences. Elle aborde quelque chose que les deux cultures partagent : une fascination permanente pour la symétrie. Pourtant, parce qu’elle englobe un si large éventail de phénomènes, la théorie des groupes est nécessairement abstraite.
Normalement, nous considérons la symétrie comme une propriété d’une forme. Mais les théoriciens des groupes se concentrent davantage sur ce que vous pouvez faire avec une forme – en particulier, toutes les façons dont vous pouvez la changer tout en conservant à l’identique. Plus précisément, ils recherchent toutes les transformations qui laissent une forme inchangée, compte tenu de certaines contraintes. Ces transformations sont appelées « symétries » de la forme. Ensemble, elles constituent un « groupe », c’est-à-dire un ensemble de transformations dont les relations définissent l’architecture la plus élémentaire de la forme.
Dans le cas d’un matelas, les transformations modifient son orientation dans l’espace (c’est ce qui change) tout en conservant sa rigidité (c’est la contrainte). Et après la transformation, le matelas doit être bien ajusté sur le cadre de lit rectangulaire (c’est ce qui reste le même). Une fois ces règles en place, voyons quelles transformations remplissent les conditions requises pour devenir membre de ce petit groupe exclusif. Il s’avère qu’il n’y en a que quatre.
La première est la transformation « ne rien faire » qui laisse le matelas comme il était au départ. Elle satisfait certainement à toutes les règles, mais elle n’aide pas beaucoup à prolonger la durée de vie de votre matelas. Pourtant, il est très important de l’inclure dans le groupe. Elle joue le même rôle pour la théorie des groupes que zéro pour l’addition de nombres, ou que 1 pour la multiplication. Les mathématiciens l’appellent « l’élément neutre », que l’on désigne dans cet article par la lettre I.
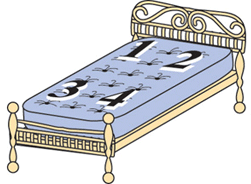 Viennent ensuite les trois véritables façons de retourner un matelas. Pour les distinguer, il est pratique d’étiqueter les coins du matelas en les numérotant ainsi :
Viennent ensuite les trois véritables façons de retourner un matelas. Pour les distinguer, il est pratique d’étiqueter les coins du matelas en les numérotant ainsi :
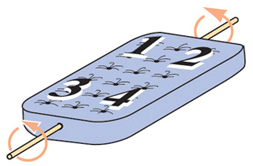 La première transformation est celle représentée au début de l’article. Le personnage essaie de faire pivoter le matelas d’un côté à l’autre en le faisant pivoter de 180° autour de son axe le plus long, dans un mouvement que nous désignons par la lettre H comme « horizontal ».
La première transformation est celle représentée au début de l’article. Le personnage essaie de faire pivoter le matelas d’un côté à l’autre en le faisant pivoter de 180° autour de son axe le plus long, dans un mouvement que nous désignons par la lettre H comme « horizontal ».
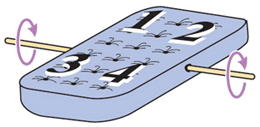 La deuxième transformation consiste à renverser le matelas par un basculement « vertical » que l’on baptisera par la lettre V. Cette manœuvre échange sa tête avec son pied. L’effet est de faire pivoter le matelas de 180° autour de son axe le plus court.
La deuxième transformation consiste à renverser le matelas par un basculement « vertical » que l’on baptisera par la lettre V. Cette manœuvre échange sa tête avec son pied. L’effet est de faire pivoter le matelas de 180° autour de son axe le plus court.
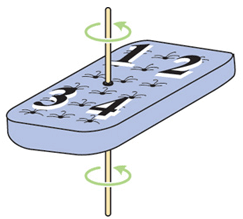 La dernière possibilité est de faire tourner le matelas d’un demi-tour tout en le maintenant à plat sur le lit. Contrairement aux transformations H et V, cette « rotation » R maintient la surface supérieure sur le dessus.
La dernière possibilité est de faire tourner le matelas d’un demi-tour tout en le maintenant à plat sur le lit. Contrairement aux transformations H et V, cette « rotation » R maintient la surface supérieure sur le dessus.
Cette différence apparaît lorsque nous observons le matelas en nous positionnant au-dessus et que l’on admet pour les besoins de l’exercice que le matelas est devenu translucide. Examinons alors les positions des quatre chiffres aux après chacune des transformations possibles.
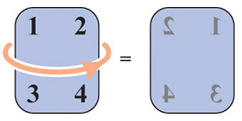 Le retournement horizontal transforme les chiffres en images miroir. Le « 1 » et le « 2 » échangent leur position ; Le « 3 » et le « 4 » échangent également leur position.
Le retournement horizontal transforme les chiffres en images miroir. Le « 1 » et le « 2 » échangent leur position ; Le « 3 » et le « 4 » échangent également leur position.
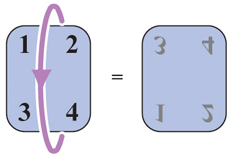 Le retournement vertical permute les nombres d’une manière différente : les couples « 1 – 2 » et « 3 – 4 » échangent leur position et apparaissent en images miroir.
Le retournement vertical permute les nombres d’une manière différente : les couples « 1 – 2 » et « 3 – 4 » échangent leur position et apparaissent en images miroir.
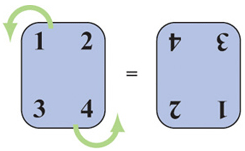 Enfin la rotation ne génère aucune image miroir. Elle renverse simplement les chiffres, échangeant cette fois « 1 » avec « 4 » et « 2 » avec « 3 ».
Enfin la rotation ne génère aucune image miroir. Elle renverse simplement les chiffres, échangeant cette fois « 1 » avec « 4 » et « 2 » avec « 3 ».
Ces détails ne sont pas le point principal. Ce qui compte, c’est les relations qui existent entre ces quatre transformations. On va faire apparaître ses relations à l’aide du diagramme suivant.
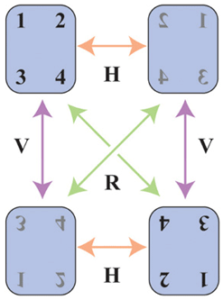 Les quatre « états » possibles du matelas sont indiqués dans les coins du diagramme. L’état supérieur gauche est le point de départ. Les flèches colorées indiquent les mouvements qui font passer le matelas d’un état à un autre.
Les quatre « états » possibles du matelas sont indiqués dans les coins du diagramme. L’état supérieur gauche est le point de départ. Les flèches colorées indiquent les mouvements qui font passer le matelas d’un état à un autre.
Par exemple, la flèche verte pointant du coin supérieur gauche vers le coin inférieur droit représente l’action de la rotation R. La même ligne verte a également une pointe de flèche à l’autre extrémité, car si vous faites R deux fois, cela revient à ne rien faire.
Cela ne devrait pas surprendre. Cela signifie simplement que le fait de placer la tête du matelas à la place du pied, puis de refaire la même rotation, ramène le matelas à son état d’origine. Nous pouvons résumer cette propriété avec l’équation RR = I, où RR signifie faire R deux fois, et I est l’élément neutre correspondant à « ne rien faire ». Dans le même ordre d’idées, les transformations de retournement horizontal et vertical opérées deux fois se neutralisent : HH = I et VV = I.
Le diagramme fournit d’autres informations. Par exemple, il montre que le retournement vertical est équivalent à HR, un retournement horizontal suivi d’une rotation. Pour vérifier cela, commencez à l’état de départ en haut à gauche. Dirigez-vous plein est le long de H jusqu’à l’état suivant, et de là, allez en diagonale sud-ouest le long de R. Vous arrivez au même état que si vous aviez simplement suivi V pour commencer, le diagramme montre que HR = V.
Notez également que l’ordre dans lequel les actions sont exécutées n’a pas d’importance : HR = RH, car les deux routes mènent à V. Cette indifférence à l’ordre est vraie pour toute autre paire d’actions. C’est la généralisation de la « commutativité » pour l’addition des nombres ordinaires que nous connaissons bien : x + y = y + x. Mais attention, le groupe des matelas est spécial. De nombreux autres groupes ne respectent pas la commutativité.
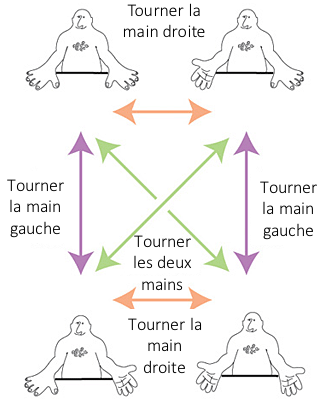 Le groupe des matelas apparaît également à certains endroits inattendus, de la symétrie des molécules d’eau à la logique d’une paire d’interrupteurs électriques. C’est l’un des charmes de la théorie des groupes. Il révèle l’unité cachée de choses qui autrement ne sembleraient pas liées… comme cette anecdote sur la façon dont le physicien Richard Feynman a obtenu un report de son enrôlement dans l’armée américaine.
Le groupe des matelas apparaît également à certains endroits inattendus, de la symétrie des molécules d’eau à la logique d’une paire d’interrupteurs électriques. C’est l’un des charmes de la théorie des groupes. Il révèle l’unité cachée de choses qui autrement ne sembleraient pas liées… comme cette anecdote sur la façon dont le physicien Richard Feynman a obtenu un report de son enrôlement dans l’armée américaine.
Le psychiatre de l’armée qui l’interrogeait a demandé à Feynman de lui tendre les mains pour pouvoir les examiner. Feynman les a sortis, une paume vers le haut, l’autre vers le bas. « Non, dans l’autre sens », lui a demandé le psychiatre. Alors Feynman inversa les deux mains, laissant une paume vers le bas et l’autre vers le haut. Si l’on considère toutes les façons possibles dont il aurait pu tendre ses deux mains, ainsi que les différentes transitions entre elles, les flèches forment le même modèle que le groupe de matelas !
Librement adapté de : https://opinionator.blogs.nytimes.com/2010/05/02/group-think/?_r=0, un article écrit par Steven Strogatz, professeur de mathématiques appliquées de la Cornell University.
