xxxx
 |
 |
 |
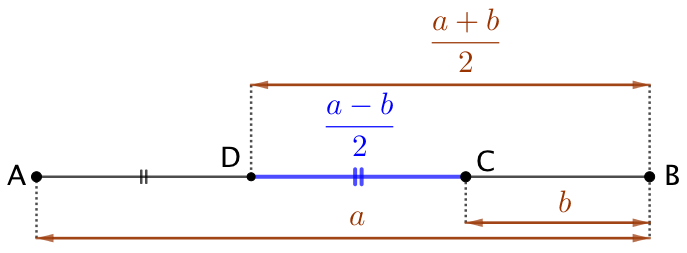
| Moyenne arithmétique : |
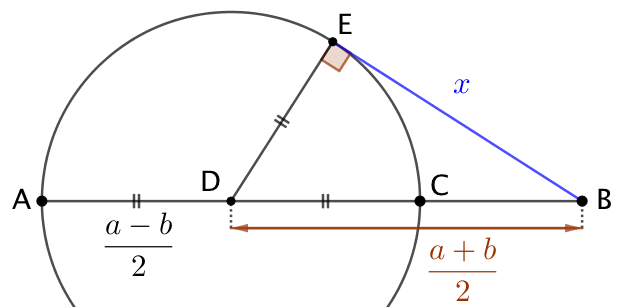
Moyenne géométrique : |
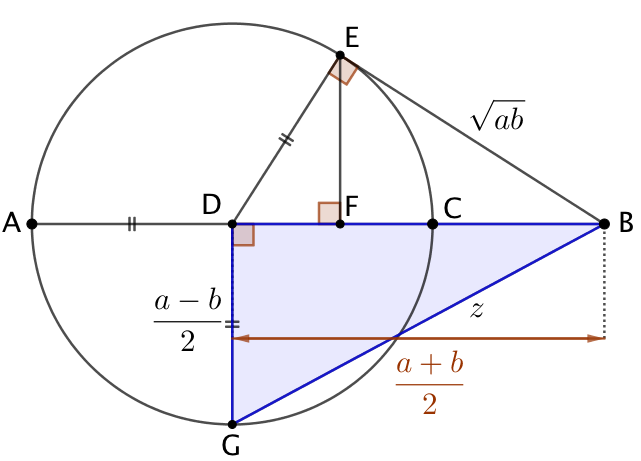
Les triangles DFE et DBE sont semblables : Moyenne harmonique : |
 |
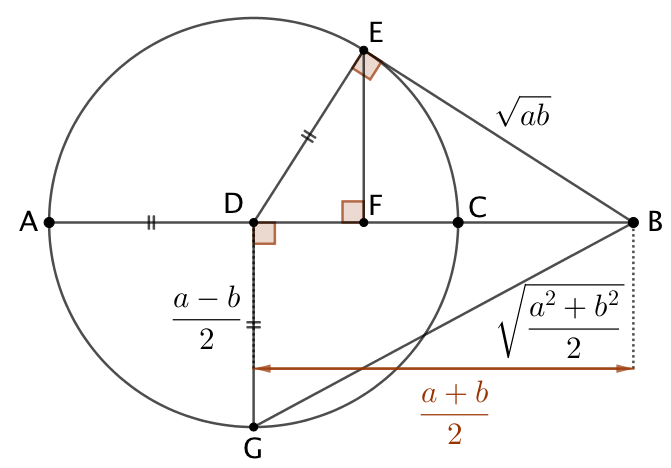 |
Moyenne quadratique : |
On observe que ![]() . Donc les moyennes classées dans l’ordre décroissant sont :
. Donc les moyennes classées dans l’ordre décroissant sont :
- la moyenne quadratique
- la moyenne arithmétique
- la moyenne géométrique
- la moyenne harmonique
