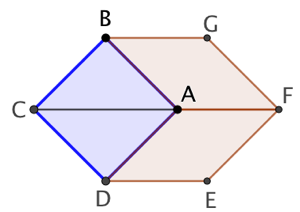
Étant donné le segment [CF], on veut construire les points A, B, D, E, G tels que A soit sur [CF], que ABCD soit un carré et que ADEF et ABGF soient des losanges.
Construction :
On remarque que la figure est symétrique par rapport à l’axe (CF). De plus, si on réussit à construire le triangle BAF, on peut le compléter par symétrie pour obtenir le losange BAFG. Donc le problème se limite à trouver une méthode de construction de la figure simplifiée de gauche. Celle-ci se compose du triangle ABC isocèle et rectangle et du triangle BAF isocèle.
- On trace un angle
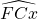de 45°. - On trace un angle
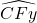de 22,5°. Par exemple en traçant la bissectrice d’un angle de sommet F et de mesure 45°. - L’intersection de [Cx) et de [Fy) est le point B.
- On trace la perpendiculaire à (CB) passant par B. Elle coupe (CF) au point A.
Explications :
ABC, moitié d’un carré, est un triangle isocèle et rectangle en B donc 
mesure 45°. ABF est un triangle isocèle de sommet A. Chaque à la base mesure la moitié de 45°, soit 22,5°.
