La racine carrée de 2 n’est pas un nombre rationnel

Voici trois raisonnements par l’absurde permettant de démontrer que \sqrt{2} \notin \mathbb{Q}.

Résultat intermédiaire : Si le carré d’un nombre entier est pair, ce nombre est pair.

Soit n \in \mathbb{N} tel que n^2 est pair. Supposons que n est impair. Alors il existe un entier naturel k tel que n=2k+1.

Par conséquent : n^2 = (2k+1)^2 = 4k^2 + 4k +1 = 2(2k^2 + 2k) + 1. Ainsi n^2 serait impair, ce qui est impossible puisqu’on a supposé que n^2 était pair. Conclusion : n est pair.

Supposons que \sqrt{2} \in \mathbb{Q}. Alors il existe deux entiers naturels p et q, premiers entre eux, tels que \sqrt{2}=\dfrac{p}{q}. Les p et q sont choisis premiers entre eux afin que \sqrt{2} soit représenté par une  fraction irréductible.

Première démonstration arithmétique :

Alors p=q \sqrt{2}, donc p^2 = 2q^2. On en déduit que p^2 est un nombre pair, et qu’alors p est aussi un nombre pair.

Il existe alors un entier naturel k tel que p=2k, donc p^2= 4k^2. Mais puisque p^2 = 2q^2, il vient que 4k^2 = 2q^2, soit q^2=2k^2.

On en déduit que, comme pour p, q est un nombre pair. Mais si p et q sont pairs, ils ne peuvent pas être premiers entre eux. On aboutit à une contradiction. L’hypothèse \sqrt{2} \in \mathbb{Q} est fausse. Conclusion : \sqrt{2} \notin \mathbb{Q}.

Seconde démonstration arithmétique :

On repart de la démonstration précédente : p^2 = 2q^2. On s’intéresse aux chiffres des unités possibles de p^2 et de 2q^2 selon le chiffre des unités de p ou de q.

q 0 1 2 3 4 5 6 7 8 9
q^2 0 1 4 9 6 5 6 9 4 1
2q^2 0 2 8 8 2 0 2 8 8 2

On observe que le chiffre des unités de 2q^2 est 0, 2 ou 8. Et que celui de p^2 (ligne q^2 du tableau) est 0, 1, 4, 5, 6,  ou 9. Donc pour que p^2 = 2q^2, il faut que ces deux expressions aient 0 comme chiffre des unités.

D’après le tableau : 2q^2 est un multiple de 10 si q est un multiple de 5, et p^2 est un multiple de 10 si p est un multiple de 10, donc de 5. Mais si p et q sont des multiples de 5, ils ne peuvent pas être premiers entre eux. On aboutit à une contradiction. L’hypothèse \sqrt{2} \in \mathbb{Q} est fausse. Conclusion : \sqrt{2} \notin \mathbb{Q}.

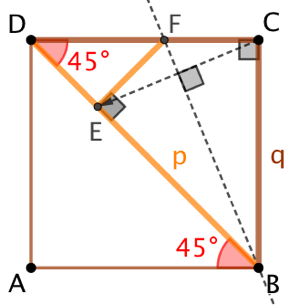Démonstration géométrique :

Soit le triangle BCD isocèle et rectangle en C tel que : BC = q et BD = p. Nous supposons que p et q sont les plus petits nombres entiers vérifiant l’égalité p^2 = 2q^2. Ce sont donc les plus petits entiers tels que BCD soit un triangle rectangle isocèle dont l’hypothèse mesure p et les deux autres cotés mesurent q.

Soit (BF) la bissectrice interne de l’angle \widehat{CBD} et considérons la symétrie d’axe (BF). Comme ABCD est un carré, l’image de C par cette symétrie est le point E qui appartient à (BD). La symétrie axiale conserve les angles et les distances. Par conséquent : BE = BC = q et \widehat{BEF} possède la même mesure que \widehat{FCB}, soit 90°.

Comme ABCD est un carré, \widehat{BDC} et \widehat{ABD} possèdent la même mesure, soit 45°. Par ailleurs \widehat{EDF} = \widehat{BDC} et \widehat{FED} = \widehat{BEF}. On en déduit que le triangle DEF est isocèle et rectangle en E.

Or DE = DB - EB = p-q qui est entier naturel. De même, DF = DC - FC = DC - FE puisque l’on considère la symétrie d’axe (BF) qui transforme C en E. Par conséquent DF = DC - DE puisque DEF est isocèle. Il vient donc que DF = q - (p - q) = 2q - p qui est aussi un entier naturel. En effet 2q > p d’après l’inégalité triangulaire appliqué au triangle BCD.

En résumé, DEF est triangle isocèle et rectangle dont les dimensions sont des entiers naturels inférieurs à p et à q. Ce qui contredit l’hypothèse que le triangle BCD était le triangle isocèle et rectangle le plus petit tel que p^2 = 2q^2. L’hypothèse \sqrt{2} \in \mathbb{Q} est fausse. Conclusion : \sqrt{2} \notin \mathbb{Q}.

Print Friendly, PDF & Email