I – Définitions et propriétés
- Une inéquation est constituée de deux expressions littérales séparées par un signe d’inégalité. Chaque expression s’appelle un membre de l’inéquation. Dans au moins une des expressions figure au moins une inconnue.
- Deux inéquations équivalentes sont deux inéquations possédant les mêmes solutions.
- Résoudre une inéquation consiste à trouver les valeurs de l’inconnue ou des inconnues pour lesquelles l’inéquation est vérifiée. En pratique, cela revient à transformer progressivement l’inéquation de départ en inéquations équivalentes de plus en plus simples.
Pour résoudre une inéquation, il faut connaitre les propriétés suivantes.
Utilité de cette propriété : Pour comparer deux nombres ou deux expressions littérales, il est parfois plus facile d’étudier le signe de leur différence.
Démonstration :
1ère partie : on suppose que ![]() et on cherche à démontrer que
et on cherche à démontrer que ![]()
1er cas : ![]() . Comme
. Comme ![]() , alors nécessairement
, alors nécessairement ![]() . L’expression
. L’expression ![]() représente la soustraction de deux nombres positifs dont le premier est plus grand que le second. Le résultat est donc positif :
représente la soustraction de deux nombres positifs dont le premier est plus grand que le second. Le résultat est donc positif : ![]()
2ème cas : ![]() . Alors
. Alors ![]() . Donc
. Donc ![]() . L’expression
. L’expression ![]() représente la somme de deux nombres positifs. Le résultat est donc positif :
représente la somme de deux nombres positifs. Le résultat est donc positif : ![]() .
.
3ème cas : ![]() . Évident.
. Évident.
Conclusion : dans tous les cas, si ![]() alors
alors ![]() .
.
2ème partie (réciproque) : On suppose à présent que ![]() et on cherche à démontrer que
et on cherche à démontrer que ![]() .
.
Raisonnons par l’absurde en supposant l’inverse de ce que l’on veut démontrer. L’inverse de ![]() est
est ![]() .
.
1er cas : ![]() impossible car alors
impossible car alors ![]() alors que nous avons supposé que
alors que nous avons supposé que ![]() .
.
2ème cas : ![]() . Alors d’après la première partie de la démonstration, on peut en déduire que
. Alors d’après la première partie de la démonstration, on peut en déduire que ![]() . Encore impossible car nous avons supposé que
. Encore impossible car nous avons supposé que ![]() .
.
En résumé, on voir que la supposition ![]() conduit à chaque fois à une contradiction. Cela signifie que cette supposition est fausse, donc que son contraire est vrai. Conclusion : si
conduit à chaque fois à une contradiction. Cela signifie que cette supposition est fausse, donc que son contraire est vrai. Conclusion : si ![]() alors
alors ![]() .
.
Autrement dit : soient ![]() trois nombres réels quelconques. Si
trois nombres réels quelconques. Si ![]() alors
alors ![]() et
et ![]() .
.
Démonstration : supposons que ![]() et démontrons alors que
et démontrons alors que ![]()
D’après la propriété précédente, pour démontrer que ![]() , on peut tout aussi bien démontrer que
, on peut tout aussi bien démontrer que ![]() .
.
Or : ![]() . Par hypothèse
. Par hypothèse ![]() donc
donc ![]() .
.
On démontre de façon similaire que si Si ![]() alors
alors ![]() .
.
Autrement dit : soient ![]() deux nombres réels quelconques et
deux nombres réels quelconques et ![]() un nombre réel strictement positif quelconque. Si
un nombre réel strictement positif quelconque. Si ![]() alors
alors ![]() et
et ![]() .
.
Démonstration : on suppose que ![]() et que
et que ![]() . On veut démontrer que
. On veut démontrer que ![]() .
.
D’après la première propriété, pour démontrer que ![]() , on peut tout aussi bien démontrer que
, on peut tout aussi bien démontrer que ![]() .
.
Or ![]() . Par hypothèse
. Par hypothèse ![]() donc
donc ![]() . De plus, nous avons supposé que
. De plus, nous avons supposé que ![]() . Donc
. Donc ![]() est le produit de deux expressions positives. Par conséquent
est le produit de deux expressions positives. Par conséquent ![]() .
.
Pour démontrer l’autre propriété : si ![]() alors
alors ![]() , il suffit simplement de constater que
, il suffit simplement de constater que ![]() et que
et que ![]() . On retombe alors sur la propriété précédente.
. On retombe alors sur la propriété précédente.
Autrement dit : soient ![]() deux nombres réels quelconques et
deux nombres réels quelconques et ![]() un nombre réel strictement négatif quelconque. Si
un nombre réel strictement négatif quelconque. Si ![]() alors
alors ![]() et
et ![]() .
.
Exemple : ![]() mais
mais ![]() puisque
puisque ![]() .
.
Démonstration : on suppose que ![]() et que
et que ![]() . On veut démontrer que
. On veut démontrer que ![]() .
.
D’après la première propriété, pour démontrer que ![]() , on peut tout aussi bien démontrer que
, on peut tout aussi bien démontrer que ![]() .
.
Or ![]() . Par hypothèse
. Par hypothèse ![]() donc
donc ![]() et par conséquent
et par conséquent ![]() . De plus, nous avons supposé que
. De plus, nous avons supposé que ![]() . Donc
. Donc ![]() est le produit de deux expressions négatives. Par conséquent
est le produit de deux expressions négatives. Par conséquent ![]() .
.
Pour démontrer l’autre propriété, on constate à nouveau que ![]() et que
et que ![]() .
.
ATTENTION : cette propriété n’est pas vraie si on remplace les additions par d’autres opérations.
Exemple : ![]() et
et ![]() , donc
, donc ![]() car
car ![]() .
.
Démonstration : On suppose que ![]() et
et ![]() et on va démontrer que
et on va démontrer que ![]()
D’après la première propriété, pour démontrer que ![]() , on peut tout aussi bien démontrer que
, on peut tout aussi bien démontrer que ![]() .
.
Or ![]() . Nous avons supposé que
. Nous avons supposé que ![]() et
et ![]() . Donc
. Donc ![]() et
et ![]() . Par conséquent
. Par conséquent ![]() est la somme de deux expressions positives, elle donc positive.
est la somme de deux expressions positives, elle donc positive.
II – Résolution des inéquation du premier degré
- Prenez votre temps : OBSERVER l’inéquation.
- Résoudre une inéquation revient à trouver des inéquations équivalentes de plus en plus simples jusqu’à arriver à l’inéquation :
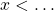 ou
ou 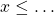 ou
ou 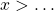 ou
ou  .
. - En général, on commence par déplacer toutes expressions contenant l’inconnue dans le membre gauche de l’inéquation et les termes constants à droite. On obtient ainsi une inéquation équivalente du type :
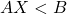 .
. - Il suffit ensuite de diviser les deux membres de l’inéquation par A en faisant attention au signe de A.
- En général, une inéquation a une infinité de solutions réparties dans un ou plusieurs intervalles
Exemple : Résoudre ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Conclusion : les solutions de l’équation ![]() est l’intervalle
est l’intervalle ![]()
III – Résolution graphique d’inéquations
1) Résolution de l’inéquation 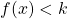
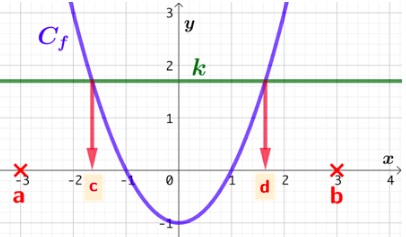 Soient la fonction f définie sur l’intervalle
Soient la fonction f définie sur l’intervalle ![]() dont la courbe représentative est
dont la courbe représentative est ![]() et
et ![]() un réel quelconque. Résoudre graphiquement l’inéquation
un réel quelconque. Résoudre graphiquement l’inéquation ![]() sur
sur ![]() , c’est trouver les abscisses de tous les points de
, c’est trouver les abscisses de tous les points de ![]() dont l’ordonnée est strictement inférieure à
dont l’ordonnée est strictement inférieure à ![]() .
.
Sur la figure de droite, on observe que l’ensemble des solutions de l’équation ![]() est l’intervalle
est l’intervalle ![]() , car pour tout
, car pour tout ![]() . Autrement dit sur l’intervalle
. Autrement dit sur l’intervalle ![]() , la courbe
, la courbe ![]() se situe en dessous de la droite horizontale des points d’ordonnée égale à
se situe en dessous de la droite horizontale des points d’ordonnée égale à ![]() .
.
Remarque : l’ensemble des solutions pour le cas ci-contre est l’intervalle ouvert ![]() car l’inéquation à résoudre est
car l’inéquation à résoudre est ![]() , c’est-à-dire que
, c’est-à-dire que ![]() doit être strictement inférieur à
doit être strictement inférieur à ![]() . Si l’inéquation avait été
. Si l’inéquation avait été ![]() , l’ensemble des solutions aurait été l’intervalle fermé
, l’ensemble des solutions aurait été l’intervalle fermé ![]() .
.
2) Résolution de l’inéquation 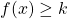
Soient la fonction f définie sur l’intervalle ![]() dont la courbe représentative est
dont la courbe représentative est ![]() et
et ![]() un réel quelconque. Résoudre graphiquement l’inéquation
un réel quelconque. Résoudre graphiquement l’inéquation ![]() sur
sur ![]() , c’est trouver les abscisses de tous les points de
, c’est trouver les abscisses de tous les points de ![]() dont l’ordonnée est supérieure ou égale à
dont l’ordonnée est supérieure ou égale à ![]() .
.
Sur la figure précédente, on observe que l’ensemble des solutions de l’équation ![]() est la réunion des intervales
est la réunion des intervales ![]() et
et ![]() , car pour tout
, car pour tout ![]() appartenant à l’un de ces deux intervalles,
appartenant à l’un de ces deux intervalles, ![]() . Autrement dit sur ces deux intervalles, la courbe
. Autrement dit sur ces deux intervalles, la courbe ![]() se situe au dessus de la droite horizontale des points d’ordonnée égale à
se situe au dessus de la droite horizontale des points d’ordonnée égale à ![]() .
.
Remarque : l’ensemble des solutions pour le cas ci-dessus sont les intervalles ![]() et
et ![]() , qui sont fermés des côtés de
, qui sont fermés des côtés de ![]() et
et ![]() car l’inéquation à résoudre est
car l’inéquation à résoudre est ![]() , c’est à dire que
, c’est à dire que ![]() doit être supérieur ou égal à
doit être supérieur ou égal à ![]() . Si l’inéquation avait été
. Si l’inéquation avait été ![]() , les intervalles auraient été ouverts des côtés de
, les intervalles auraient été ouverts des côtés de ![]() et
et ![]() .
.
3) Résolution de l’inéquation 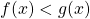
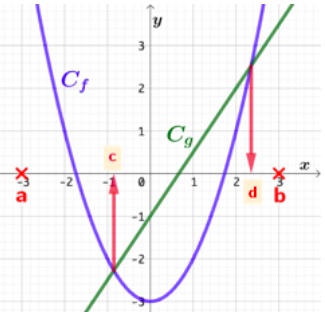 Soient deux fonctions
Soient deux fonctions ![]() et
et ![]() définies sur l’intervalle
définies sur l’intervalle ![]() dont les courbes représentatives sont
dont les courbes représentatives sont ![]() et
et ![]() .
.
Résoudre l’inéquation ![]() , c’est trouver les abscisses de tous les points de
, c’est trouver les abscisses de tous les points de ![]() dont les ordonnées sont strictement inférieures à celles des points de
dont les ordonnées sont strictement inférieures à celles des points de ![]() possédant la même abscisse.
possédant la même abscisse.
Dans l’exemple ci-contre, on observe que la courbe ![]() est en dessous de la courbe
est en dessous de la courbe ![]() sur l’intervalle
sur l’intervalle ![]() . Cet intervalle est la solution de l’inéquation.
. Cet intervalle est la solution de l’inéquation.
