I – Identités remarquables
Soient ![]() ,
, ![]() ,
, ![]() , trois nombres réels quelconques :
, trois nombres réels quelconques : ![]()
Soient ![]() ,
, ![]() ,
, ![]() ,
, ![]() , quatre nombres réels quelconques :
, quatre nombres réels quelconques : ![]()
Vocabulaire :
- Développer, c’est transformer un produit de facteurs en une somme de termes.
- Factoriser, c’est transformer une somme de termes en un produit de facteurs.
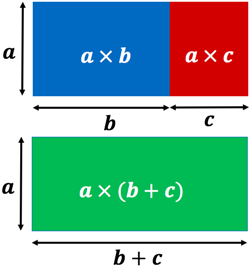 Démonstration :
Démonstration :
La distributivité simple se comprend aisément à l’aide de la figure de droite, en considérant que l’on calcule des aires de deux façons différentes.
La distributivité double n’est qu’une conséquence de la distributivité simple que l’on applique deux fois :
![]()
Certaines égalités littérales, toujours vraies, obtenues en appliquant la distributivité de la multiplication par rapport à l’addition, sont appelées identités remarquables.
Soient ![]() et
et ![]() , deux nombres réels quelconques :
, deux nombres réels quelconques :
![]()
Il faut connaître ces identités dans les deux sens : de gauche à droite pour développer, de droite à gauche pour factoriser.
Démonstration : (a+b)^2 = (a+b)(a+b) = a^2 + ab + ba + b^2 = a^2 + 2ab + b^2
Les deux autres identités remarquables se démontrent de la même façon en prenant garde aux signes.
Illustration géométrique des identités remarquables :
Les nombres réels ![]() et
et ![]() représentent des distances donc sont positifs.
représentent des distances donc sont positifs.
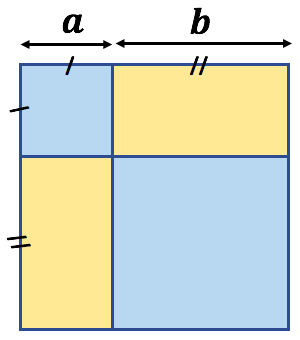 Première identité remarquable :
Première identité remarquable : ![]()
L’aire du petit carré bleu est ![]()
L’aire du grand carré bleu est ![]()
L’aire de chaque rectangle jaune est ![]()
L’aire du grand carré de côté ![]() est la somme des aires des deux carrés bleus et des deux rectangles jaunes :
est la somme des aires des deux carrés bleus et des deux rectangles jaunes :
ce qui donne : ![]()
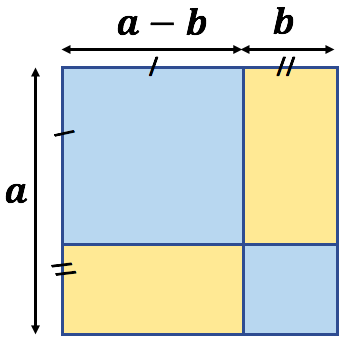 Deuxième identité remarquable :
Deuxième identité remarquable : ![]()
L’aire du grand carré bleu est ![]()
L’aire du petit carré bleu est ![]()
L’aire de chaque rectangle jaune est ![]()
L’aire du grand carré de côté ![]() est la somme des aires des deux carrés bleus et des deux rectangles jaunes :
est la somme des aires des deux carrés bleus et des deux rectangles jaunes :
![]() , donc
, donc ![]() , soit
, soit ![]() .
.
Après simplification il vient : ![]() .
.
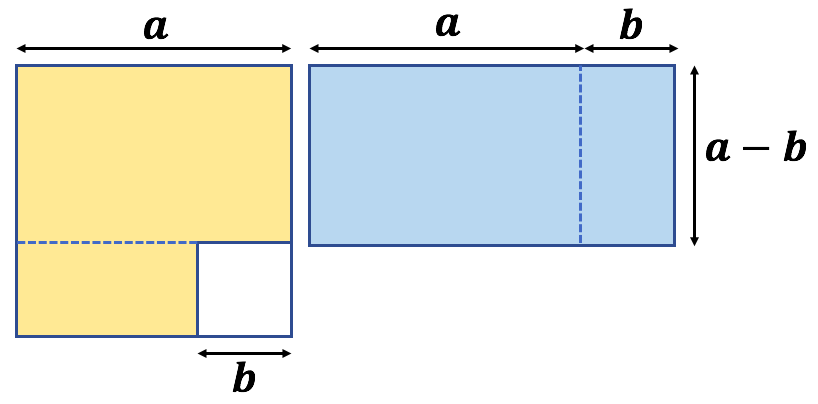 Troisième identité remarquable :
Troisième identité remarquable : ![]()
L’aire bleue : ![]()
L’aire jaune est égale à l’aire du carré jaune et blanc de côté ![]() dont on aurait découpé le petit carré blanc de côté
dont on aurait découpé le petit carré blanc de côté ![]() , soit
, soit ![]() .
.
II – Résolutions d’équations
- Une équation est constituée de deux expressions littérales séparées par un signe d’égalité. Chaque expression s’appelle un membre de l’équation. Dans au moins une des expressions figure au moins une inconnue.
- Deux équations équivalentes sont deux équations possédant les mêmes solutions.
- Résoudre une équation consiste à trouver les valeurs de l’inconnue ou des inconnues pour lesquelles les deux membres sont égaux. En pratique, cela revient à transformer progressivement l’équation de départ en équations équivalentes de plus en plus simples.
Exemples :
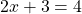 . Cette équation possède une inconnue :
. Cette équation possède une inconnue : 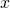 , qui ne figure que dans le membre de gauche.
, qui ne figure que dans le membre de gauche.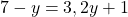 . Cette équation possède une inconnue :
. Cette équation possède une inconnue : 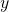 , qui figure dans les deux membres.
, qui figure dans les deux membres.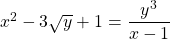 . Cette équation possède deux inconnues :
. Cette équation possède deux inconnues : 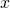 et
et 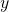 , qui figurent dans les deux membres.
, qui figurent dans les deux membres.
- Prenez votre temps : OBSERVER l’équation.
- Résoudre une équation revient à trouver des équations équivalentes de plus en plus simples jusqu’à arriver à l’équation :
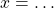 .
. - On exclut les valeurs impossibles de l’inconnue, c’est-à-dire celles qui ne permettent pas de calculer les membres de l’équation. En général il s’agit
- des valeurs qui annulent le dénominateur d’une fraction ou
- des valeurs pour lesquelles l’expression se trouvant sous le symbole de la racine est négative.
- On cherche un facteur commun à tous les termes.
- On tente de simplifier lex expressions littérales à l’aide des identités remarquables.
- On combine ces deux dernières méthodes.
- On cherche à obtenir une équation sans dénominateur en multipliant les deux membres par une expression littérale.
- Il est souvent intéressant de transformer l’équation afin que le second membre soit égal à 0.
- Si aucune des méthodes ne fonctionne, on peut essayer de développer les expressions, puis de simplifier.
- On résout l’équation en ne conservant que les valeurs qui n’ont pas été exclues.
Méthode générale de résolution d’une équation du premier degré :
La forme générale d’une équation du premier degré est : ![]() , ou
, ou ![]() et
et ![]() sont deux réels, avec
sont deux réels, avec ![]() .
.
![]() . Possible car
. Possible car ![]() . La solution unique de l’équation
. La solution unique de l’équation ![]() est
est ![]() .
.
![]() . La solution de l’équation
. La solution de l’équation ![]() est
est ![]() .
.
L’idée est de faire passer les inconnues dans le membre de gauche de l’équation et les termes constants (sans inconnue) dans le membre de droite.
![]()
La solution de l’équation ![]() est
est ![]() .
.
Méthodes de résolution d’équation n’étant pas du premier degré
L’idée est de transformer cette équation en une ou plusieurs équations du premier degré.
Équations du type : 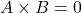
![]()
Équations du type : 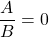
![]() .
.
Équations du type : 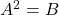
- 1er cas :
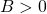 alors
alors 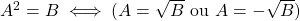
- 2ème cas :
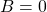 alors
alors 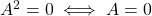
- 3ème cas :
 alors l’équation n’a pas de solution car un carré ne peut être égal à un nombre négatif.
alors l’équation n’a pas de solution car un carré ne peut être égal à un nombre négatif.
On remarque que ![]() .
.
Méthode n°1 : ![]() . On sait que deux nombres qui ont le même carré sont égaux ou opposés.
. On sait que deux nombres qui ont le même carré sont égaux ou opposés.
Donc ![]() ou
ou ![]() . Les solutions de l’équation
. Les solutions de l’équation ![]() sont
sont ![]() .
.
Méthode n°2 : On fait passer tous les termes dans le membre de gauche.
![]() . On reconnait une identité remarquable.
. On reconnait une identité remarquable.
![]() . Un produit de facteurs est nul si au moins un des facteurs est nul.
. Un produit de facteurs est nul si au moins un des facteurs est nul.
![]() ou
ou ![]() ou
ou ![]()
L’erreur serait de développer puis de simplifier, car alors on se retrouverait avec une équation du second degré dont la résolution est au programme de pemière.
Il faut rechercher un facteur commun. Dans notre exemple, il n’est pas évident mais on peut le faire apparaître grâce à une identité remarquable. On remarque que ![]() .
.
L’équation à résoudre devient alors : ![]() . Il y a un facteur commun :
. Il y a un facteur commun : ![]() .
.
On factorise le membre de gauche de l’équation : ![]() .
.
À l’intérieur des crochets, il n’y a aucun facteur commun évident. Il nous reste à développer l’expression figurant entre crochets.
L’équation devient ![]() . Puis on simplifie l’expression entre crochets.
. Puis on simplifie l’expression entre crochets.
L’équation devient ![]() ou
ou ![]() ou
ou ![]() .
.
Les solutions de l’équation ![]() sont
sont ![]() .
.
Le membre de gauche présente une fraction dont le dénominateur s’annule pour ![]() . Nous devons donc supposer dans la suite de la résolution que
. Nous devons donc supposer dans la suite de la résolution que ![]() ne peut pas s’annuler. Si l’une des solutions trouvées est 0, il ne faudra pas la retenir comme valable.
ne peut pas s’annuler. Si l’une des solutions trouvées est 0, il ne faudra pas la retenir comme valable.
On va se débarrasser du dénominateur en multipliant les deux membres de l’équation par ce dénominateur :
![]()
On reconnait l’identité remarquable : ![]() .
.
Notre équation devient alors : ![]() . La solution de l’équation
. La solution de l’équation ![]() est
est ![]() .
.
III – Un peu d’histoire
 Un problème que se posaient des babyloniens environ 1800 ans avec J.C.
Un problème que se posaient des babyloniens environ 1800 ans avec J.C.
J’ai additionné le côté et la surface de mon carré : 20. Quel est le côté ?
Aujourd’hui, on détermine cette quantité en traduisant la situation par l’équation suivante : ![]() . La solution de cette équation est : 4.
. La solution de cette équation est : 4.
 Un problème que se posaient des égyptiens un peu plus tard sur un papyrus :
Un problème que se posaient des égyptiens un peu plus tard sur un papyrus :
Une quantité, ses ![]() , son
, son ![]() donnent 19.
donnent 19.
Aujourd’hui, on détermine cette quantité en traduisant la situation par l’équation suivante : ![]() . La solution de cette équation est 10,5.
. La solution de cette équation est 10,5.
 |
 |
 |
| Diophante d’Alexandrie (IIIe siècle)
Le premier à donner un nom à l’inconnue d’une équation : |
François Viète (XVIe siècle)
Le premier à écrire une équation avec des symboles qui remplacent une phrase. |
René Descartes (XVIIe siècle)
Le premier à désigner l’inconnue d’une équation par la lettre |
