Le centre d’un groupe est le sous-groupe constitué des éléments commutant avec tous les éléments du groupe.
Sous-groupe engendré
Soit A une partie d’un groupe G. Il existe un plus petit sous-groupe de G contenant A. On l’appelle sous-groupe engendré par A et on le note ![]() . Définition explicite :
. Définition explicite : ![]() .
.
Conjugaison et automorphisme intérieur d’un groupe :
Soit ![]() , l’application
, l’application ![]() sur G définie par
sur G définie par ![]() est un automorphisme intérieur de G. L’application de
est un automorphisme intérieur de G. L’application de ![]() de G dans Aut(G) qui à tout élément
de G dans Aut(G) qui à tout élément ![]() de G fait correspondre l’automorphisme intérieur
de G fait correspondre l’automorphisme intérieur ![]() est un morphisme de groupe dont le noyau est le centre de G et dont l’image est un sous-groupe distingué de Aut(G).
est un morphisme de groupe dont le noyau est le centre de G et dont l’image est un sous-groupe distingué de Aut(G).
Éléments conjugués : Deux éléments d’un groupe G sont conjugués si l’un est l’image de l’autre par un automorphisme intérieur. La relation “être conjugué” est une relation d’équivalence dans G.
La conjugaison dans un groupe peut s’interpréter comme une action de ce groupe sur lui-même.
Sous-groupes conjugués : Deux sous-groupes sont conjugués si l’un est l’image de l’autre par un automorphisme intérieur.
Théorème de Cayley :
Tout groupe G est isomorphe à un sous-groupe du groupe symétrique S(G) des permutations de G. Si G est un groupe fini d’ordre ![]() , il est isomorphe à un sous-groupe de
, il est isomorphe à un sous-groupe de ![]() .
.
Théorème de Lagrange :
Si ![]() sous-groupe de
sous-groupe de ![]() , alors
, alors ![]() .
.
Si ![]() sous-groupe de
sous-groupe de ![]() et
et ![]() sous-groupe de
sous-groupe de ![]() , alors
, alors ![]() .
.
Sous-groupes distingués ou normaux
Un sous-groupe H d’un groupe G est un sous-groupe distingué, ou normal, s’il est stable par tout automorphisme intérieur, c’est-à-dire si ![]() . Autre définition :
. Autre définition : ![]() ou
ou ![]() .
.
Le noyau d’un morphisme de groupe est un sous-groupe distingué. Dans un groupe abélien, tous les sous-groupes sont distingués. Le centre d’un groupe est un sous-groupe distingué.
Groupe quotient
Soit H un sous-groupe distingué de G. On définit une relation d’équivalence sur G : ![]() . G/H est le groupe quotient constitué des classes d’équivalences. La classe d’équivalence de
. G/H est le groupe quotient constitué des classes d’équivalences. La classe d’équivalence de ![]() est
est ![]() .
.
L’application p de G dans G/H qui à un élément ![]() fait correspondre sa classe d’équivalence
fait correspondre sa classe d’équivalence ![]() est un morphisme de groupe surjectif, appelé la surjection canonique de G/H.
est un morphisme de groupe surjectif, appelé la surjection canonique de G/H.
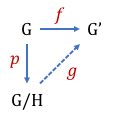 Propriété universelle du quotient :
Propriété universelle du quotient :
Soient H un sous-groupe distingué de G et ![]() un morphisme du groupe G vers le groupe G’. Si
un morphisme du groupe G vers le groupe G’. Si ![]() , il existe un morphisme unique
, il existe un morphisme unique ![]() de G/H vers G’ tel que
de G/H vers G’ tel que ![]() . De plus
. De plus ![]() et
et ![]() .
.
Cas particulier : Si ![]() . Alors
. Alors ![]() est injectif et le morphisme de
est injectif et le morphisme de ![]() vers
vers ![]() est un isomorphisme.
est un isomorphisme.
Groupe fini :
Tout sous-ensemble fini et stable d’un groupe est un sous-groupe.
On dit qu’un groupe est de type fini s’il admet une partie génératrice finie. L’ordre d’un groupe fini est son cardinal ou est égal à l’infini.
L’ordre d’un élément de d’un groupe fini est l’ordre du groupe engendré par cet élément. Si l’ordre de ![]() est
est ![]() , cela signifie que
, cela signifie que ![]() est le plus petit entier naturel tel que
est le plus petit entier naturel tel que ![]() .
.
Si ![]() alors
alors ![]() .
.
Propriété : Si H est un sous-groupe de G, de type fini et si G/H est aussi de type fini, alors G est de type fini.
Groupe monogène :
C’est groupe engendré par un seul élément. Un groupe monogène est isomorphe à ![]() s’il est infini ou à
s’il est infini ou à ![]() s’il possède un nombre fini d’éléments.
s’il possède un nombre fini d’éléments.
Un groupe cyclique est un groupe monogène d’ordre fini. Si l’ordre de ![]() est
est ![]() alors
alors ![]() .
.
Actions de groupe :
Une action (à gauche) d’un groupe G sur un ensemble E est une application G x E dans E qui à tout ![]() fait correspondre
fait correspondre ![]() , telle que
, telle que ![]() et
et ![]() .
.
Soit ![]() et
et ![]() le groupe des bijections sur E. L’application
le groupe des bijections sur E. L’application ![]() sur E définie par
sur E définie par ![]() est une bijection. On définit le morphisme de groupes
est une bijection. On définit le morphisme de groupes ![]() de
de ![]() dans
dans ![]() par
par ![]() .
.
Soit G opérant sur E.
Orbite : On définit une relation d’équivalence sur E par ![]() . La classe d’équivalence d’un élément
. La classe d’équivalence d’un élément ![]() est
est ![]() , appelée Orbite de
, appelée Orbite de ![]() . Une action de groupe ne possédant qu’une seule orbite est dénommée transitive.
. Une action de groupe ne possédant qu’une seule orbite est dénommée transitive.
Un sous-ensemble A de E est dit invariant ou stable pour l’action de G si et seulement si ![]() . Les orbites correspondent aux plus petits sous-ensembles non vides de E qui sont invariants pour l’action de G. Un sous-ensemble invariant est forcément une réunion d’orbites.
. Les orbites correspondent aux plus petits sous-ensembles non vides de E qui sont invariants pour l’action de G. Un sous-ensemble invariant est forcément une réunion d’orbites.
Stabilisateur : Le stabilisateur de ![]() est le sous-groupe de G défini par
est le sous-groupe de G défini par ![]() . Le stabilisateur de
. Le stabilisateur de ![]() est un sous-groupe distingué de G.
est un sous-groupe distingué de G.
Propriété : Soient le groupe ![]() opérant sur un ensemble
opérant sur un ensemble ![]() , et
, et ![]() :
:
-
- Il y a une bijection entre
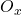 et
et 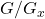
- En particulier, si
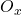 est fini, alors son ordre est l’indice de
est fini, alors son ordre est l’indice de 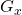 , c’est-à-dire l’ordre de
, c’est-à-dire l’ordre de 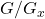 .
. - Si
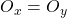 alors
alors 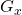 et
et 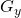 sont conjugués.
sont conjugués. - Si
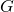 et
et 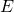 sont finis, l’ordre de E est la somme des indices de tous ses stabilisateurs.
sont finis, l’ordre de E est la somme des indices de tous ses stabilisateurs.
- Il y a une bijection entre
