I – Vocabulaire de base
1) Droite, demi-droite et segment
| Figure | Notation | Signification |
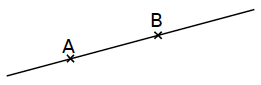
| Lire : « segment [AB] ».
C’est le segment d’extrémités A et B. |
||
 |
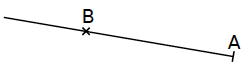
Lire : « droite (AB) ».
C’est la droite qui passe par les points A et B. |
|
 |
Lire : « demi-droite [AB) ».
C’est la demi-droite d’origine A passant par le point B. |
|
 |
|
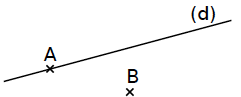
Le point A appartient à la droite (d).
Le point B n’appartient pas à la droite (d). |
2) Points alignés
- Par un point, il passe une infinité de droites.
- Deux points sont toujours alignés.
- Par deux points, il ne passe qu’une seule droite.
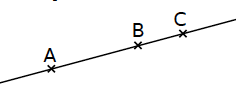 Exemple : Les points A, B et C sont alignés.
Exemple : Les points A, B et C sont alignés.
II – Coder une figure
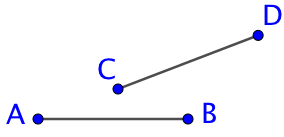 Une figure de géométrie n’est jamais parfaite ou elle n’est pas assez parlante. Ainsi dans la figure de droite, rien ne prouve que les distances AB et CD sont égales. On peut les mesurer à la règle mais ce n’est jamais très précis. Si on mesure AB = 30 mm et CD = 31 mm, on peut croire que les deux distances ne sont pas égales. Or elles le sont.
Une figure de géométrie n’est jamais parfaite ou elle n’est pas assez parlante. Ainsi dans la figure de droite, rien ne prouve que les distances AB et CD sont égales. On peut les mesurer à la règle mais ce n’est jamais très précis. Si on mesure AB = 30 mm et CD = 31 mm, on peut croire que les deux distances ne sont pas égales. Or elles le sont.
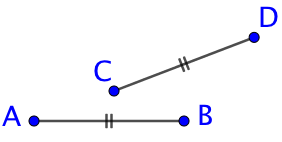 On indique sur la figure les propriétés des objets que l’on trace à l’aide de petits signes. Par exemple pour signifier que deux segments possèdent la même longueur, on ajoute le même signe sur les deux segments. Ces codes sont particulièrement utiles pour les figures effectuées à main levée, c’est-à-dire sans instrument.
On indique sur la figure les propriétés des objets que l’on trace à l’aide de petits signes. Par exemple pour signifier que deux segments possèdent la même longueur, on ajoute le même signe sur les deux segments. Ces codes sont particulièrement utiles pour les figures effectuées à main levée, c’est-à-dire sans instrument.
On rencontrera dans la suite d’autres codages très utiles.
III – Reporter une longueur au compas
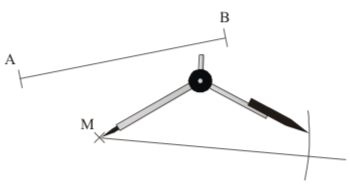
Le compas ne sert pas qu’à tracer des cercles : il sert aussi à reporter des longueurs. Reporter des longueurs permet de construire plusieurs segments de même longueur, de doubler, tripler des longueurs,…
Exemple : [AB] est un segment et M un point, on va construire un autre segment [MN] de même longueur que [AB].
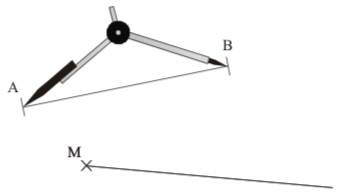 |
 |
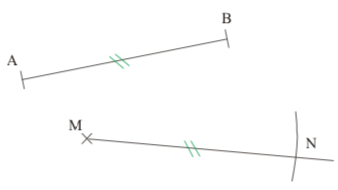 |
| On trace une demi-droite d’origine |
On pique en |
On nomme |
EXERCICES
- 3 / 96 : Placer des points
- 4 / 96 : Tracer des droites, segments
- 5 / 96 : Appartenance et alignement
- 20 / 98 : Frise
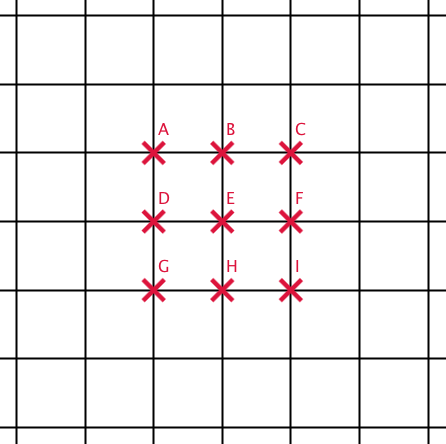 Défi n°1 : Recopier la figure ci-contre. Relier tous les points de cette figure sans lever le crayon et en dessinant seulement quatre segments.
Défi n°1 : Recopier la figure ci-contre. Relier tous les points de cette figure sans lever le crayon et en dessinant seulement quatre segments.

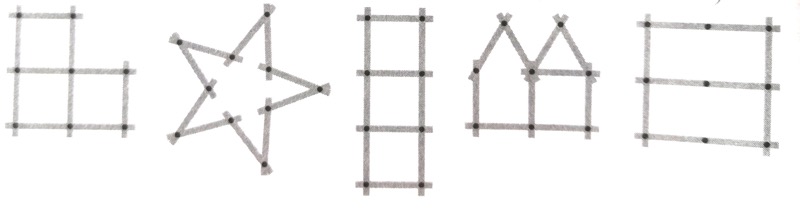
Défi n°2 : Manon joue avec un mètre plan en 10 morceaux. Laquelle des cinq figures ne peut-elle pas faire avec ce mètre pliant ?