Formule de Héron

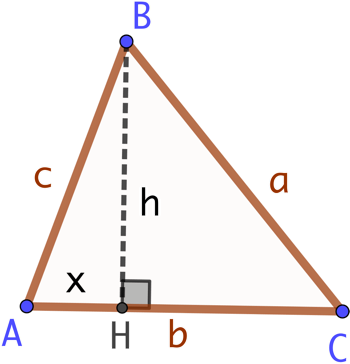
La formule de Héron permet de calculer l’aire d’un triangle quelconque dont on ne connait que les longueurs des trois côtés : a, b et c.

En posant que le demi-périmètre du triangle est p = \dfrac{a+b+c}{2}, l’aire du triangle est A = \sqrt{p(p-a)(p-b)(p-c)}.

Explications : 

On exprime la valeur de h^2 en utilisant Pythagore sur les triangles ABH et HBC.
c^2=x^2+h^2 d’une part et a^2=(b-x)^2+h^2 d’autre part.
Ce qui donne : h^2 = c^2-x^2 = a^2-b^2-x^2+2bx. Soit x=\dfrac{c^2+b^2-a^2}{2b}.
On injecte x dans h^2 : h^2 = c^2-x^2 = c^2-\dfrac{(c^2+b^2-a^2)^2}{(2b)^2}.
h^2 = \dfrac{(2bc)^2-(c^2+b^2-a^2)^2}{(2b)^2}
h^2 = \dfrac{(2bc-c^2-b^2+a^2)(2bc+c^2+b^2-a^2)}{(2b)^2}
h^2 = \dfrac{(a^2-(b-c)^2)((b+c)^2-a^2)}{(2b)^2} = \dfrac{(a-b+c)(a+b-c)(b+c-a)(b+c+a)}{(2b)^2}
h^2 = \dfrac{(2p-2b)(2p-2c)(2p-2a)(2p)}{(2b)^2} = \dfrac{16(p-b)(p-c)(p-a)p}{(2b)^2}
\dfrac{h^2b^2}{4} = (p-b)(p-c)(p-a)p}. Or l’aire du triangle est A = \dfrac{hb}{2}.
Par conséquent A^2 = (p-b)(p-c)(p-a)p. Ce qui permet de conclure que A = \sqrt{p(p-a)(p-b)(p-c)}.

Print Friendly, PDF & Email