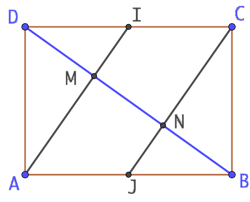
 Soient ABCD un rectangle, I et J milieux respectifs des segments [CD] et [AB]. La droite (BD) rencontre les droites (AI) et (JC) aux points M et N. On va démontrer que la condition pour que les angles en M et en N soient droits est :
Soient ABCD un rectangle, I et J milieux respectifs des segments [CD] et [AB]. La droite (BD) rencontre les droites (AI) et (JC) aux points M et N. On va démontrer que la condition pour que les angles en M et en N soient droits est : ![]() .
.
Explications :
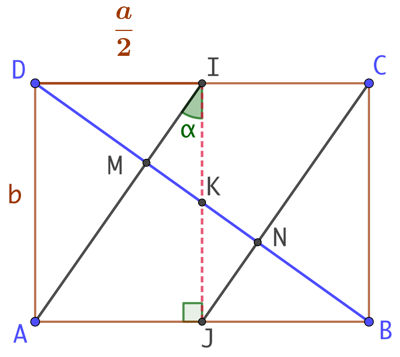
Posons ![]() et supposons que
et supposons que ![]() .
.
![]() .
.
Le théorème de Thales : ![]() .
.
Posons ![]() et
et ![]() et utilisons le théorème de Pythagore :
et utilisons le théorème de Pythagore :
Alors ![]() .
.
et ![]() .
.
Ainsi ![]() . Or
. Or ![]() .
.
Donc ![]() . En posant l’égalité des produits en croix et en simplifiant, il vient
. En posant l’égalité des produits en croix et en simplifiant, il vient ![]() , c’est-a-dire :
, c’est-a-dire : ![]() .
.
Explications par les coordonnées :
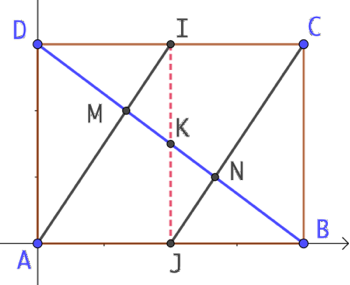 On se place dans un repère orthonormé de centre A dans lequel les points ont les coordonnées suivantes :
On se place dans un repère orthonormé de centre A dans lequel les points ont les coordonnées suivantes :
![]() .
.
Le coefficient directeur de la droite (AI) est ![]() . Celui de la droite (DK) est
. Celui de la droite (DK) est ![]() .
.
Les droites (AI) et (DK) sont perpendiculaires si le produit de leur coefficient directeur est égal à -1. Ce qui donne : ![]() , soit
, soit ![]() .
.
Remarque : les feuilles de papier au format de la série A, comme le A4, sont des rectangles possédant cette propriété.